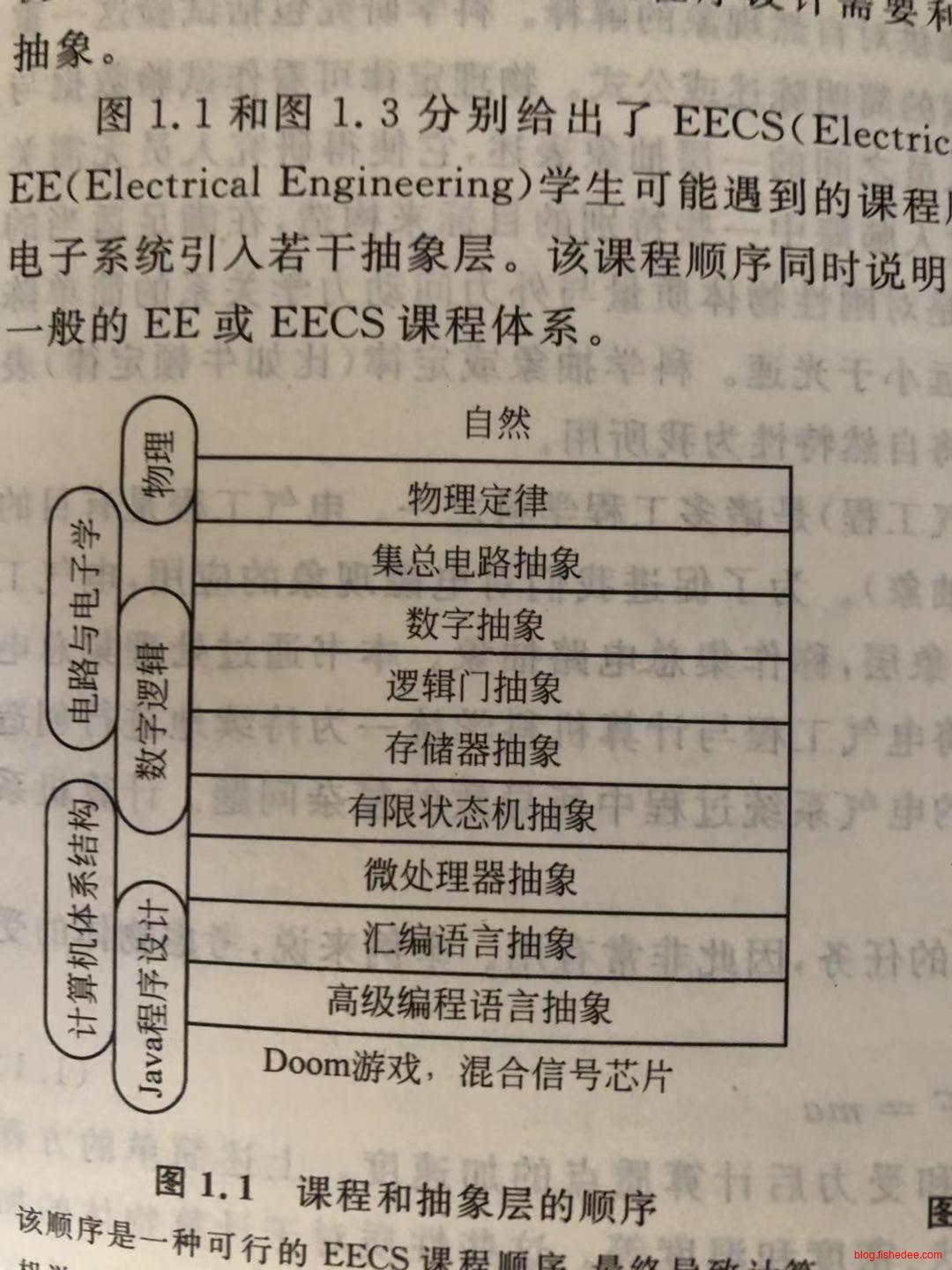
1 概述
这本由Anant Agarwal著作的书相当给力,循序渐进,相当容易理解
2 电路抽象
抽象是一种力量,它能让我们抽取部分问题的共性,并将这类共性的问题用更加简单的方法来解决。这意味着:
- 可以用更简单的方法,更上层的方法来看待问题
- 这种方法所能解决的问题是局部的,部分的,有前提的
2.1 集总电路抽象
麦克斯韦方程,是电子电路中的最底层的物理法则。所有的电子电路都可以由麦克斯韦方程来求解,但是,这样做过于复杂。因此,我们引入了满足一系列性质下的电子电路称为集总电路。而集总电路的特点是,它能用更为简洁的方程来描述电子电路,大大提高了电子电路分析和应用的效率。
集总元件的约束:
- 对集总元件边界的选择需要在所有时刻使元件与外部任何闭环链接的磁链的变化率为零
- 对集总元件边界的选择需要在所有时刻使元件内部总的随时间变化的电荷量为零
- 感兴趣的信号的时间尺度比电磁波通过集总元件时的传播延迟长得多
集总电路的约束:
- 所有时刻与电路任意部分磁链的变化率均为零
- 所有时刻电路任意节点上电荷的变化率必须为零
- 信号的时间范围必须远大于电磁波通过电路的传播延迟
当一个电路满足集合电路的约束时,它就可以用更简洁的公式来描述,例如是基尔霍夫电压定律(KVL)和基尔霍夫电流定律(KCL)
2.2 二端元件
2.2.1 电池
电池是一种特殊的元件,它有标称电压,总能量和内阻。
\[ P = VI \]
电池的功率,单位是瓦特
\[ w' = pT \]
电池的电量就是功率与时间的乘数,常见的是\(1 W \cdot s = 1 J\),还有\(1 W \cdot h\)。由于常见的电池的电压是固定的,电量可以看成是1小时内最大放电电流的数值,也就是$1 mA h $
2.2.2 线性电阻
\[ v = iR \]
普通电阻均服从欧姆定律
\[ R = \rho \frac {l}{a} \]
一段材料的电阻,与它的横截面积\(a\)成反比,与它的长度\(l\)成正比,固定的材料电阻特性称为电阻率\(\rho\)
\[ R = \rho \frac {L}{WH}\\ 对于一个立方体而言,它的电阻特性如上式所示\\ R_0 = \rho \frac {1}{1H} = \rho \frac {1}{H}\\ 对于长和宽都是1的立方体,它的电阻就是R_0\\ R = \frac {L}{W} R_0\\ 那么立方体的电阻与它的单位正方体的电阻的关系如上式所示 \]
因此,立方体电阻的特性是,它的电阻与\(R_0\)有关,与长宽比例有关,与实际的长或宽的数值无关。
2.3 关联变量约定
我们在分析电路时,我们是从元件开始分析,然后再分析包含这些元件的电路。分析元件时,我们肯定需要确定它的电流与电压的变量。但是,我们也要注意到的是,电流和电压这些变量不仅仅只有数值,还有方向。
就像要指定一个向量的方向前,我们需要先确定参考系一样。我们有约定的指定元件两端的电流和电压变量的参考系的方法。元件的电流的正方向必须是从元件的接线两端中电压的正方向的位置,指向元件本身
这句话简单的说明两个要点:
- 电流的正方向和电压的正方向是可以随意指定的
- 但是电流的正方向,必须与电压的正方向相匹配。不能从电压的正方向流入元件的方向,作为电流的负方向。
\[ p = vi \]
在关联变量的约定下,元件的瞬时功率的公式如上。注意,这个公式已经考虑了电流和电压的方向特性,当功率为正数时,元件在消耗功率,当功率为负数时,元件在提供功率。
\[ w = \int_{t_1}^{t_2}vidt \]
在关联变量的约定下,元件的在某段时间的消耗能量为如上
2.4 理想二端元件
2.4.1 导线
理想导线的电阻为0,
2.4.2 电压源与电流源
- 理想电压源提供恒定的电压V,且没有内部电阻
- 理想电流源提供恒定的电流I,且没有内部电阻。
2.4.3 电阻
理想电阻的电阻值恒定不变,不会因为两端提供的电压或电流的大小所改变。
3 电阻网络
3.1 术语
- 节点,两个或更多元件之间的连接点。注意,导线不能称为元件,所以导线与电阻之间的连接点不是节点。
- 支路,节点之间的连接称作电路的支路。注意,支路是跨过元件的。
- 回路,电路中沿着支路的闭合路径。
3.2 基尔霍夫定律
3.2.1 基尔霍夫电流定律
KCL,电路中流出任何一个节点的电流一定等于流入该节点的电流。即流入任意节点的支路电流的代数和一定为零。
一般来说,N个节点的电路只有N-1种独立的KCL方程组
3.2.2 基尔霍夫电压定律
KVL,网络中任何闭合路径上支路电压的代数和一定为零。
一般来说,N个节点和B条支路的电路只有B-N+1种独立的KVL方程组
3.2.3 电路分析基本方法
电路分析的基本方法
- 根据关联变量约定,标注每个元件的电流和电压
- 根据每个元件,写出它们的元件定律。这个时候有B个方程组
- 写出基尔霍夫定律,写出N-1个KCL和B-N+1个KVL,共B个方程组
- 联立以上的2B方程组,求解2B个未知变量,就是每个元件两端的电压和电流即可。
3.3 基于能量的分析方法
基于能量的电路分析方法
- 电路中若干元件提供的能量等于其他元件消耗的能量
- 系统的总能量在两个不同时间相同
3.4 基于串联和并联的分析方法
将电路看成是串联和并联的电路的任意组合结果
\[ R_s = R_1 + R_2 + ... + R_n \]
多个电阻串联的等效电阻\(R_s\),串联起到分压作用
\[ \frac {1} {R_s} = \frac {1} {R_1}+\frac {1} {R_2}+...+\frac {1} {R_n} \]
多个电阻并联的等效电阻\(R_s\),并联起到分流作用
3.5 基于对称的分析方法
- 将电路旋转,如果电路依然保持不变,则证明电路中部分路径是互相等效的。
- 如果电路中部分节点的电位相同,那将这些节点用理想导线连接起来后,电路的特性依然会保持不变。
3.6 基于顺序分析方法
当受控端,和控制端没有其他外部耦合的方法时,我们可以用顺序法来分步分析电路
- 首先,在假设受控端不存在时的控制端电路,并单独分析控制端的电路
- 然后,将控制端的结果转移到受控端的电源,然后单独分析受控端的电路
4 网络定理
基于KVL和KCL,我们能从理论上推导出所有的电路的结果,但是要列的方程组未知参数太多。我们进一步使用节点法来简化和求解电路。另外一方面,对于线性电路,我们发现出更为简单的方法来简化和求解。
4.1 节点法
4.1.1 一般步骤
- 选择一个被称为地的参考节点,所有电压的测量都相对该节点。定义其电位为0V。
- 标注其余节点关于地节点的电位。将任何通过独立电压源或受控电压源连接到地节点的节点标注为电压源的电压值。其余节点的电压构成待求解的未知量,需要进行标注。
- 为每个具有未知节点电压的节点列写KCL方程,地节点和通过电压源连接到地的节点无需列写。
- 求解第3步得到的方程,求得未知的节点电压。
- 反过来求解支路电压和支路电流。
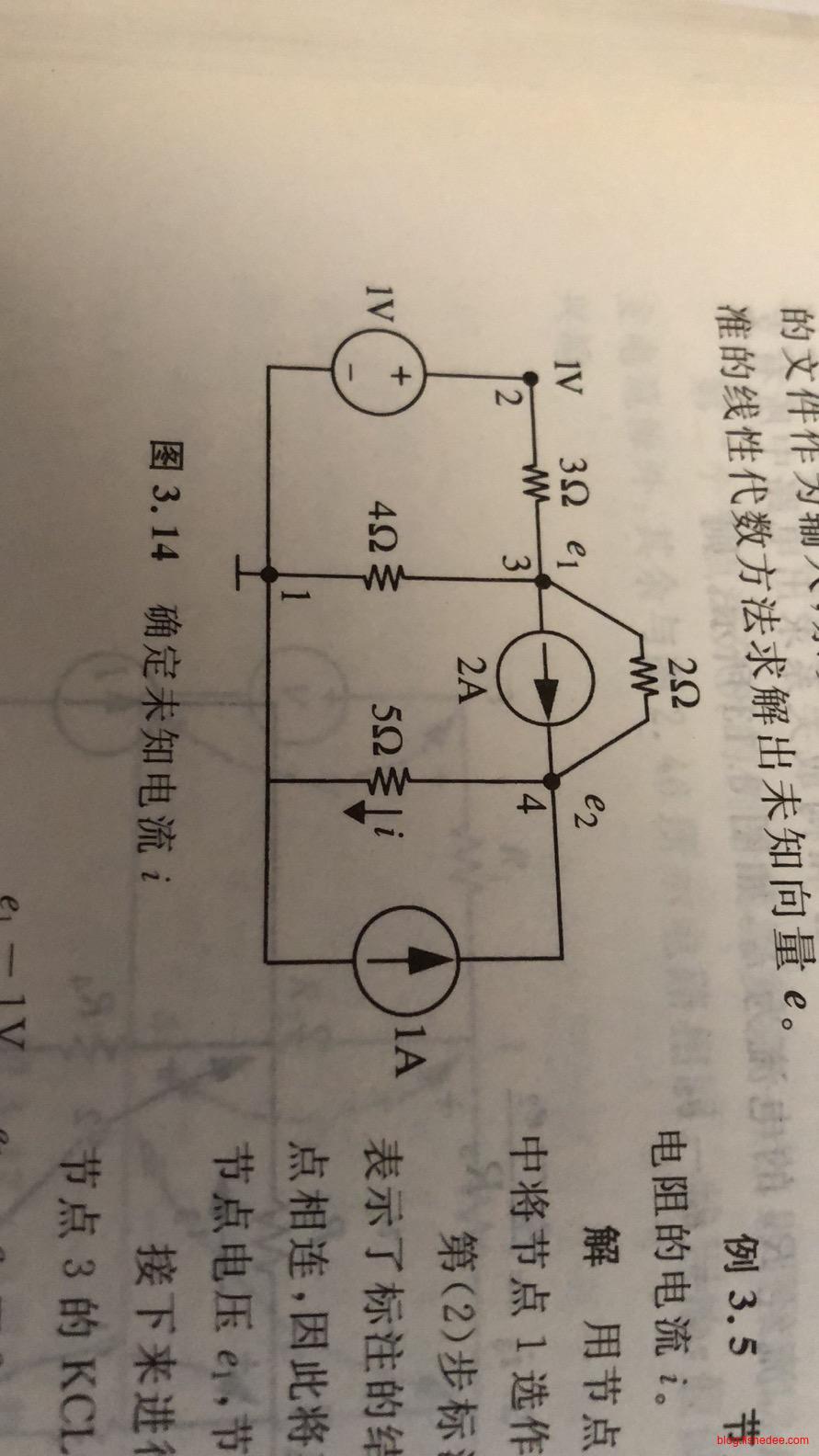
例如,在上图中,首先标注下面的节点为地节点,然后标注与地节点连接的电压源的电压值。对节点3和节点4运用KCL方程得到
\[ \frac {e_1-1V} {3 \Omega} + \frac {e_1} {4 \Omega} + \frac {e_1-e_2} {2 \Omega} + 2A = 0\\ -2A + \frac {e_2-e_1} {2 \Omega} + \frac {e_2} {5 \Omega} -1A = 0 \]
求得:
\[ e_1 = 0.65V\\ e_2 = 4.75V\\ i = 4.75/5=0.95A \]
4.1.2 浮动电压源
浮动电压源,就是没有任何接线端直接或通过其他独立电压源与地节点连接的独立电压源。独立电压源的直接运用节点法分析会失败,因为无法在独立电压源相连的节点上执行KCL,你无法指定出流过独立电压源的电流是多少。解决办法是,将独立电压源两端的节点合并为一个超节点,对这个超节点执行KCL。
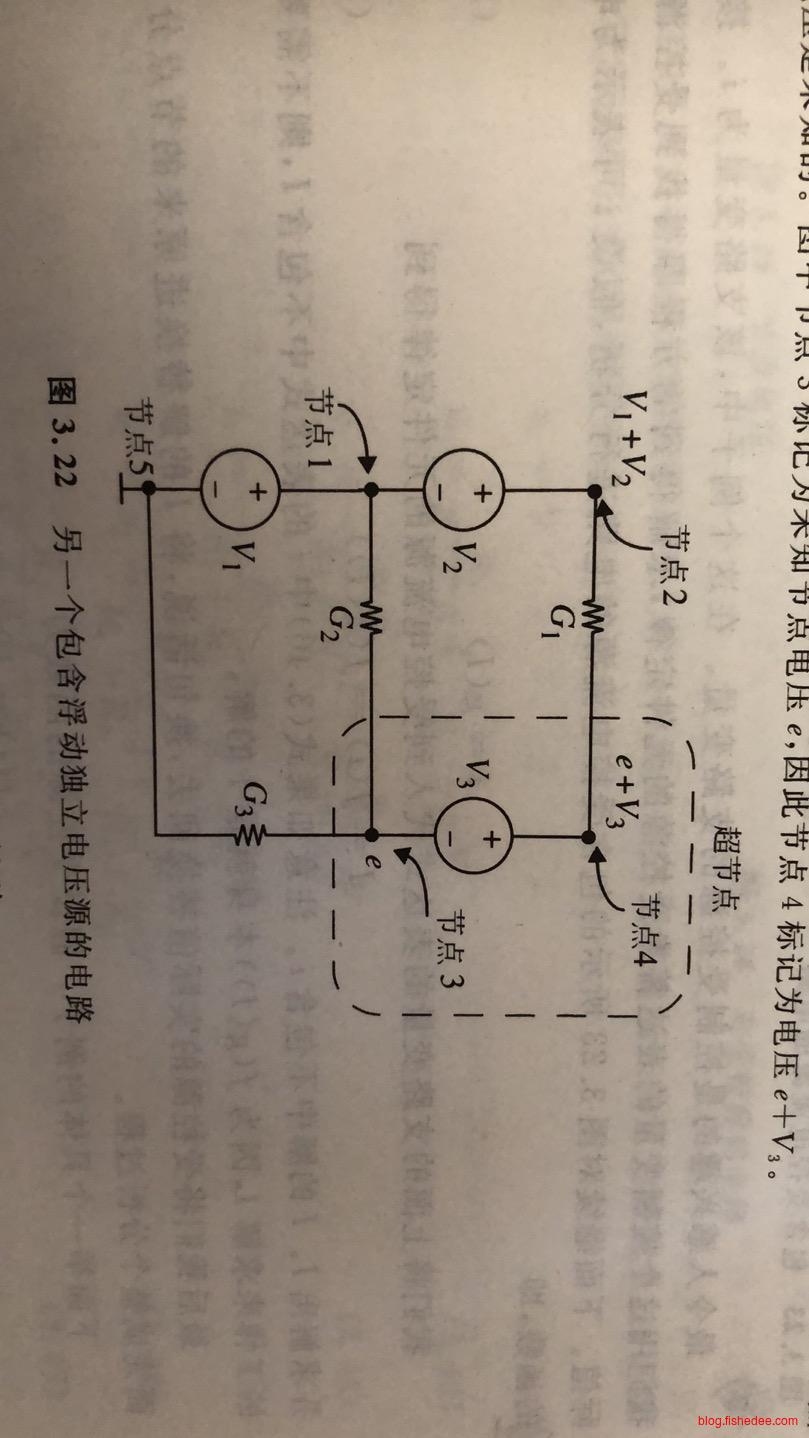
对节点3和节点4执行超节点合并,则可以列出以下方程:
\[ G_1[(e+V_3) - (V_1+V_2)] + G_2(e-V_1) + G_3 e = 0 \]
求得
\[ e = \frac {(G_1+G_2)V_1+G_1V_2-G_1V_3} {G_1+G_2+G_3} \]
4.1.3 受控电路
受控电路应用节点法,和普通的方法类似,仅需要将受控的电压源和电流源,用\(f(x)\)代替即可。要注意,这种方法并不是对所有的受控电路都能使用,必要时还需要回归到KVL和KCL。
4.2 线性系统
如果\(f(x)\)是某个激励\(x\)的响应,则线性系统的充要条件为:
\[ f(ax_1+bx_2) = af(x_1)+bf(x_2) \]
如果电路仅由电压源,电流源和线性元件构成的,则该电路肯定为线性电路。
对于线性电路,我们可以进一步使用更简单的抽象方法,叠加原理和戴维南定理
4.2 叠加原理
4.2.1 一般步骤
叠加原理:在有若干独立电源的线性网络中,可根据每个独立电源单独作用,其余独立源置为零所求得的响应纸鹤来获得电路的响应。
- 为每个独立源构成一个其余独立源置为零的子电路。将电压源置为零意味着用短路替换电压源,将电流源置为零意味着开路代替电流源。(因为两端电压为零就是短路,两端电流为零就是开路)
- 对于每个给定独立源对应的子电路,求该独立源单独作用的响应。这一步求得若干子响应。
- 通过将这些子响应相加求得全响应。
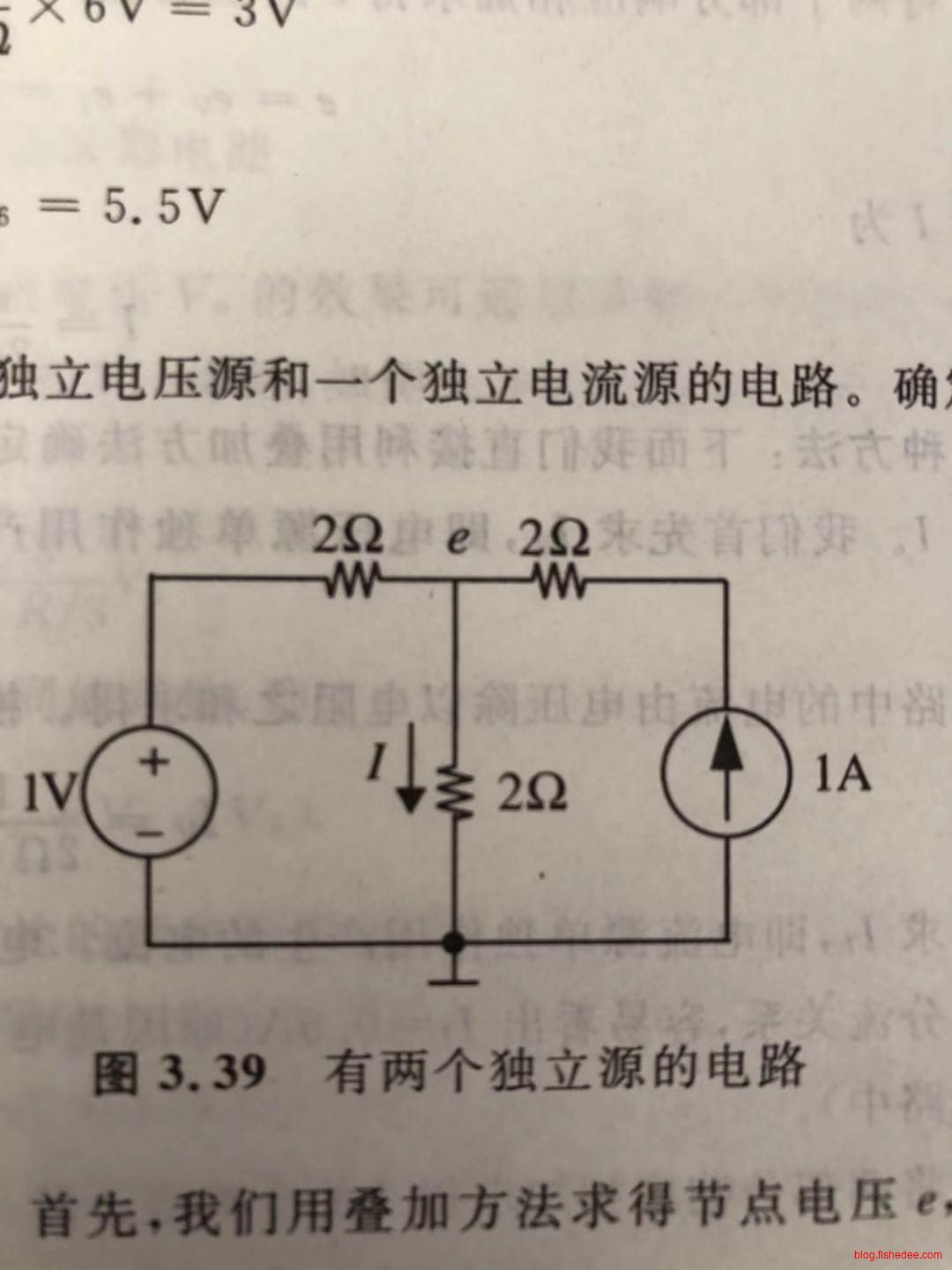
例如,我们要求上图中的\(I\)。
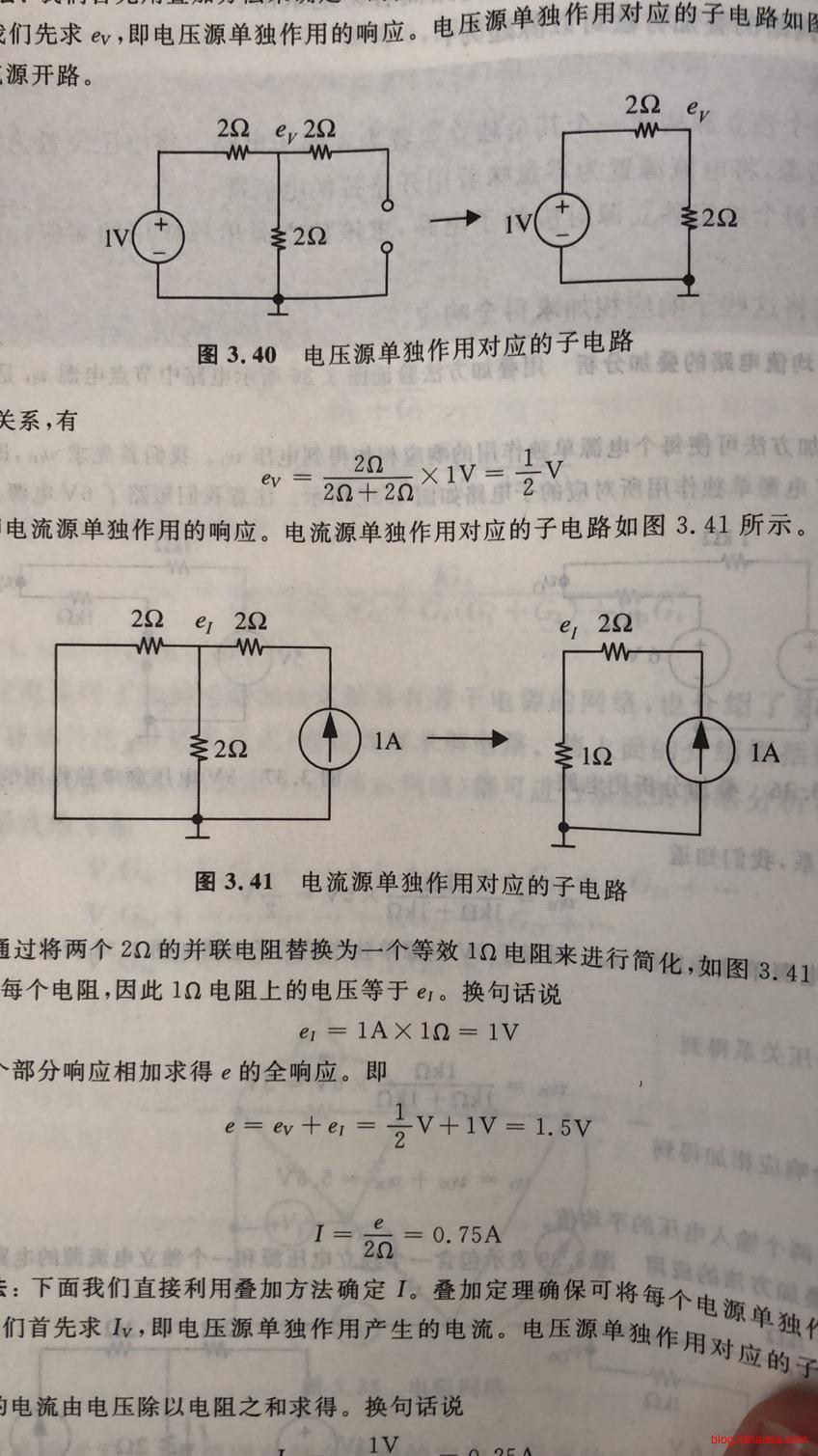
首先单独求左边的电压源,其他电源置为零产生的响应,根据分压定律,计算到\(e_v=\frac {1} {2} V\)。
然后单独求右边的电流源,其他电源置为零产生的响应,根据串并联分析方法,计算得到\(e_I = 1 V\)。
所以,合共电压为\(1.5V\),所要求得的电流为\(0.75A\)。
4.2.2 受控源的叠加规则
对于包含有受控源的电路,我们要使用叠加原理时。就是在电路中保留受控源,然后每次求解一个独立源作用(将其他独立源置为零)产生的响应,并将单独作用的响应相加得到全响应。
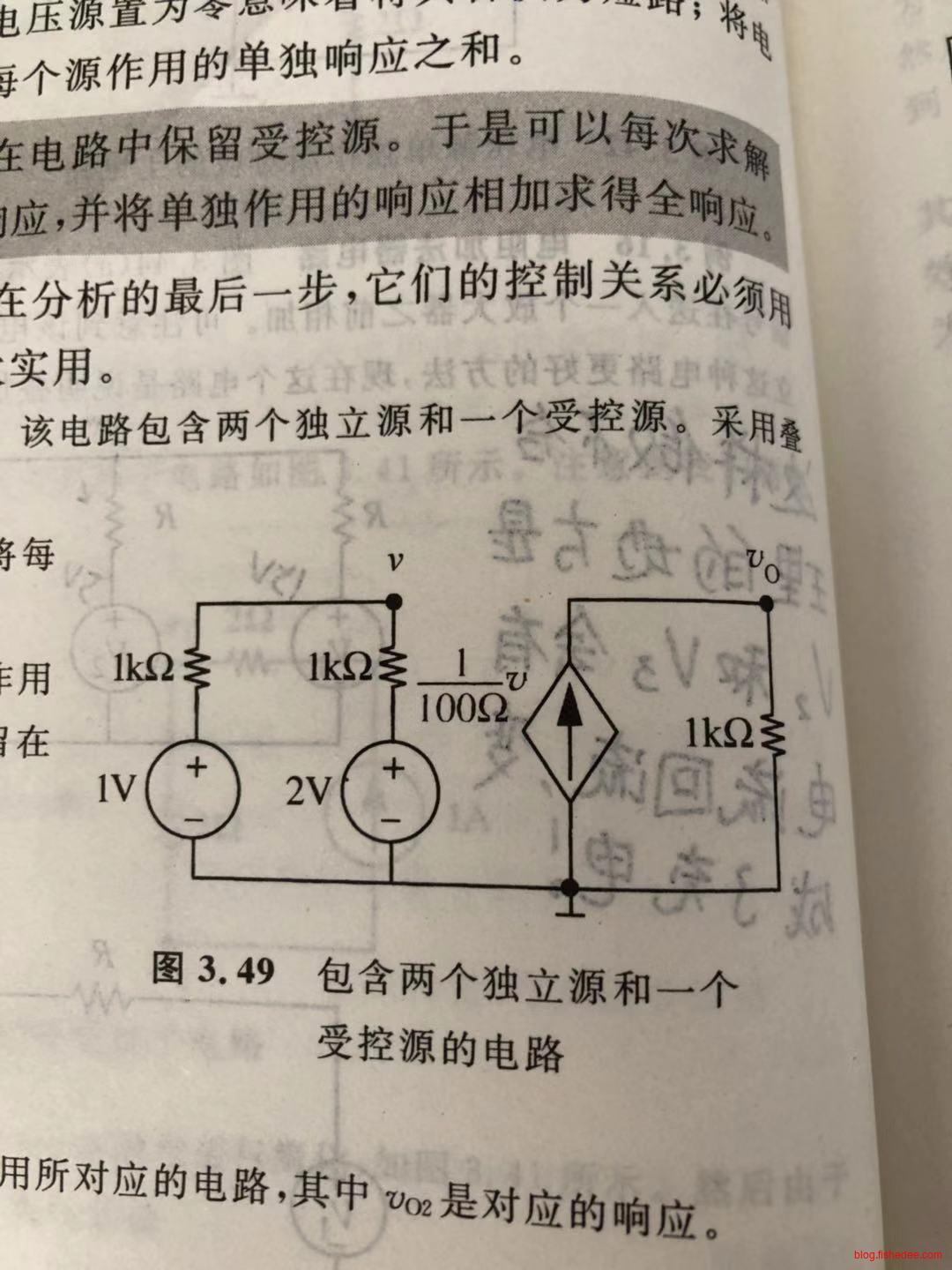
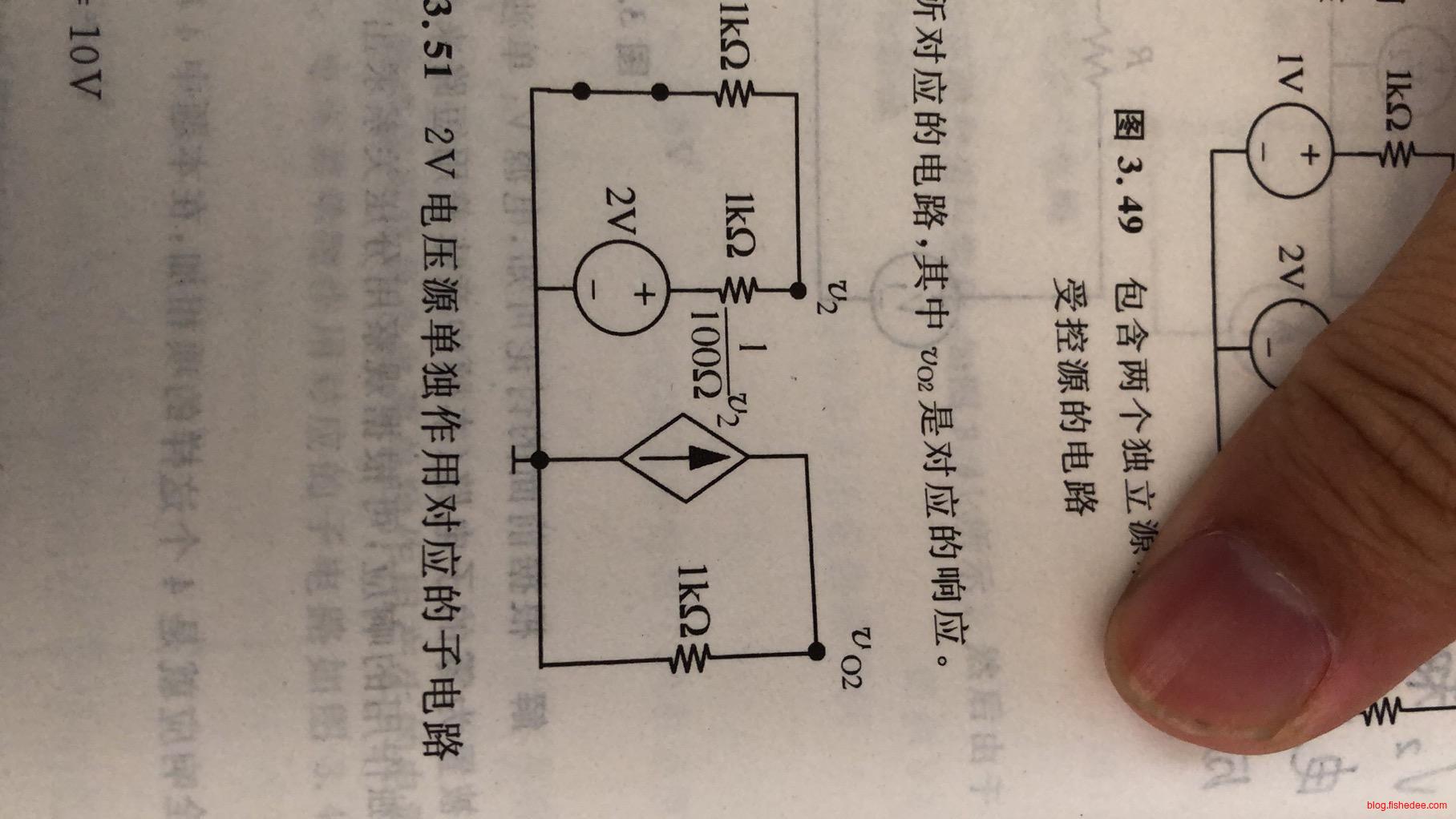
例如,我们要求图中的\(v_0\)
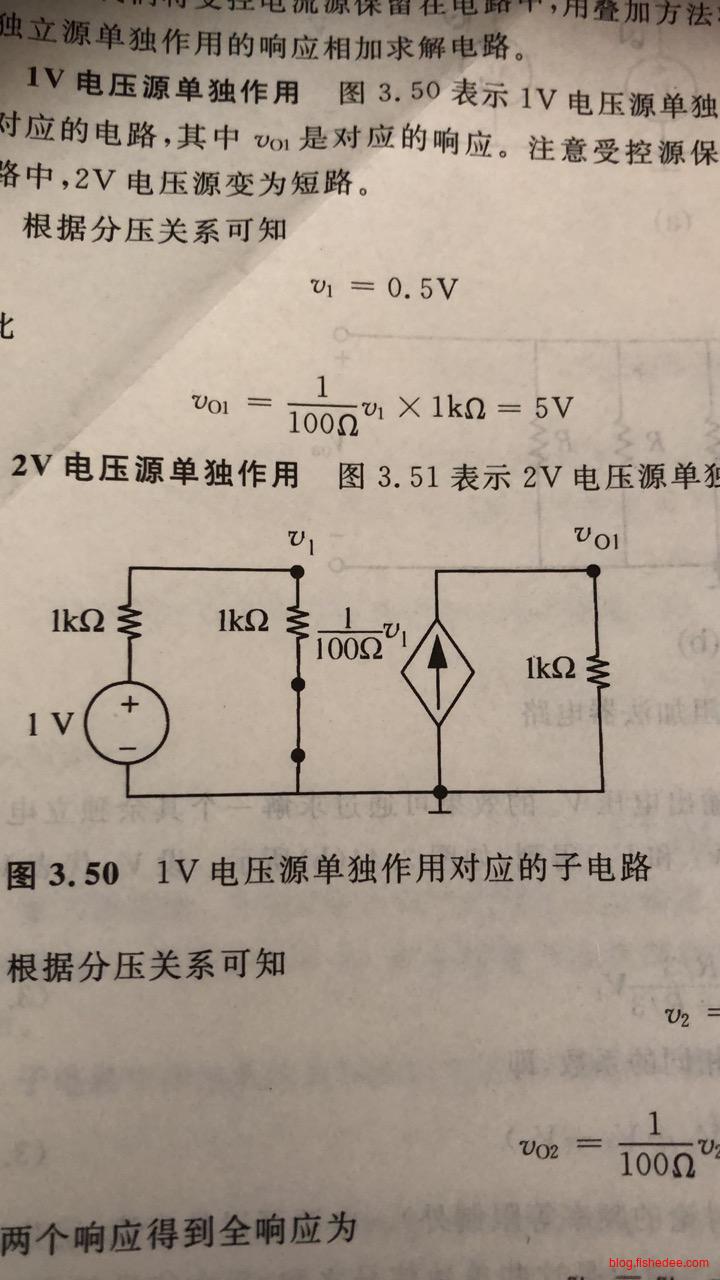
首先,保留受控源,只计算左边的电压源产生的响应。
\[ v_1 = 0.5V\\ v_{O1} = \frac {1} {100 \Omega} v_1 \times 1k\Omega = 5V \]
然后,保留受控源,只计算右边的电压源产生的响应。
\[ v_2 = 1V\\ v_{O2} = \frac {1} {100 \Omega} v_2 \times 1k\Omega = 10V \]
所以,总的结果为:
\[ v_O = v_{O1} + v_{O2} = 15V \]
4.3 戴维南定理和诺顿定理
4.3.1 一般步骤
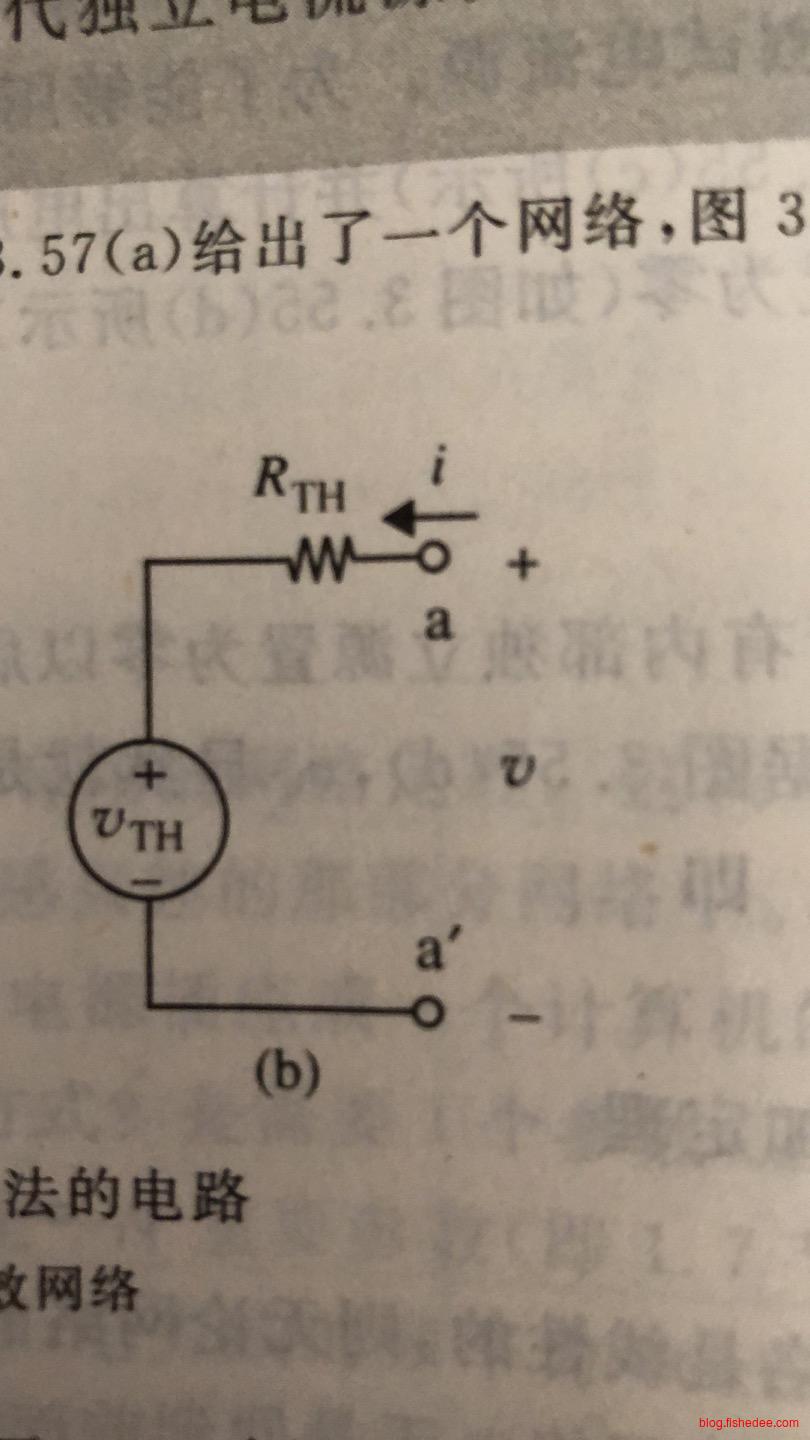
戴维南定理:任意线性网络在一对给定接线端上的戴维南电路包括一个电压源\(V_{TH}\)和一个电阻\(R_{TH}\)的串联。电压源\(V_{TH}\)和电阻\(R_{TH}\)的求解方法如下:
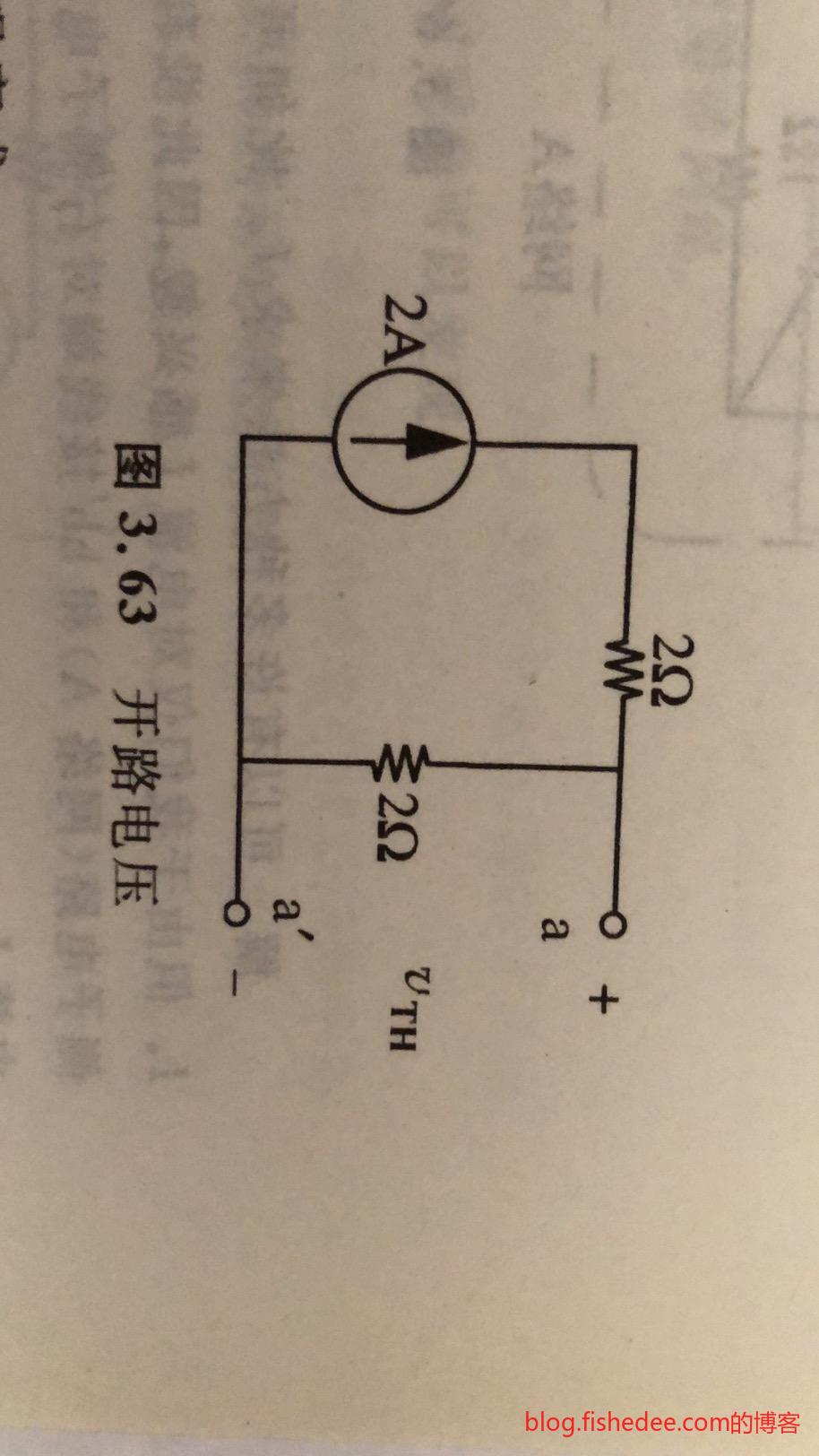
- \(V_{TH}\)可通过原网络在给定接线端对上计算或测量开路电压得到
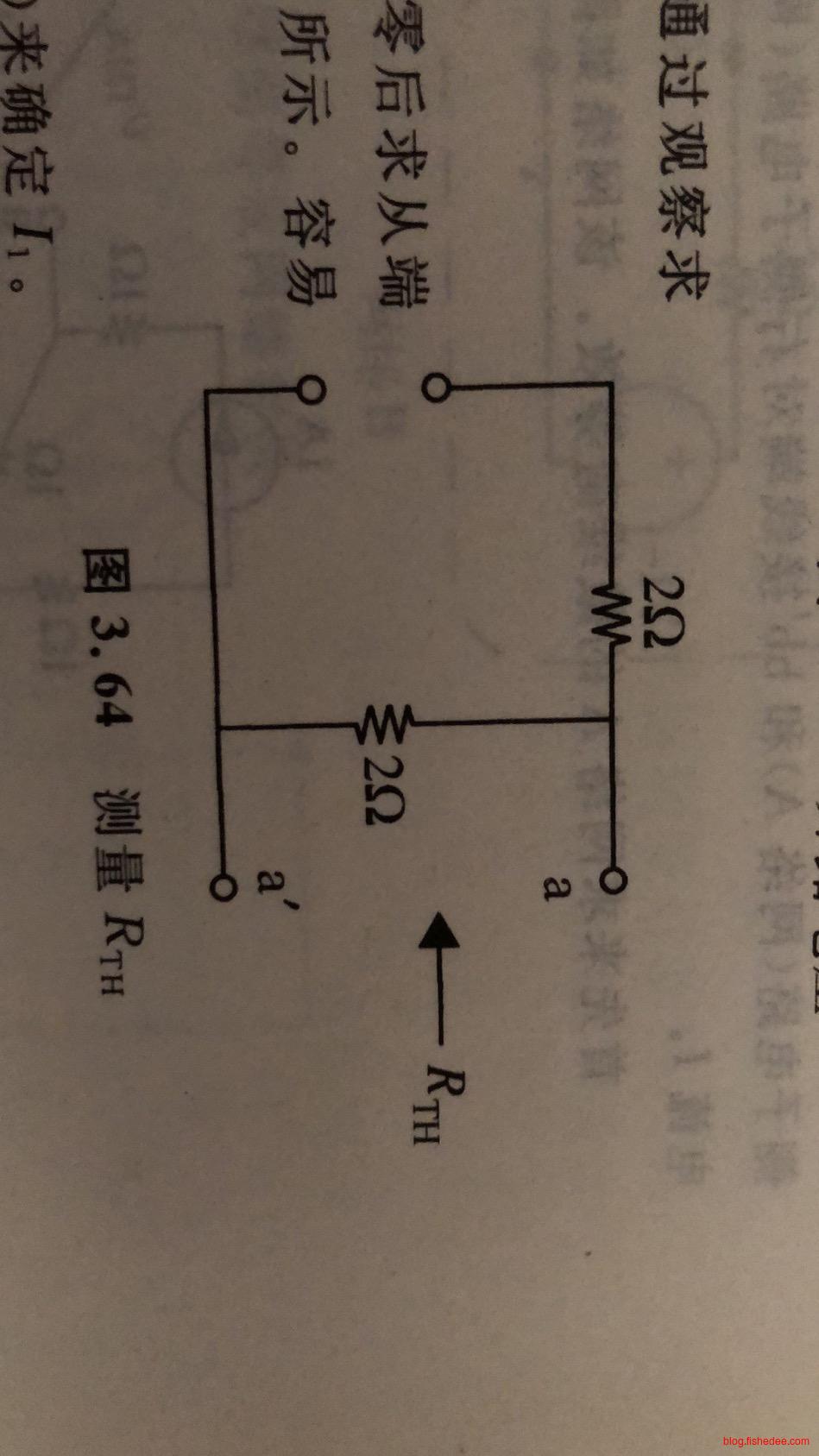
- \(R_{TH}\)可通过将原网络内部所有独立源置为零后计算或测量从接线端对看进去的电阻得到。即用短路代替独立电压源,用开路来代替独立电流源,但是受控源需要保持不变。
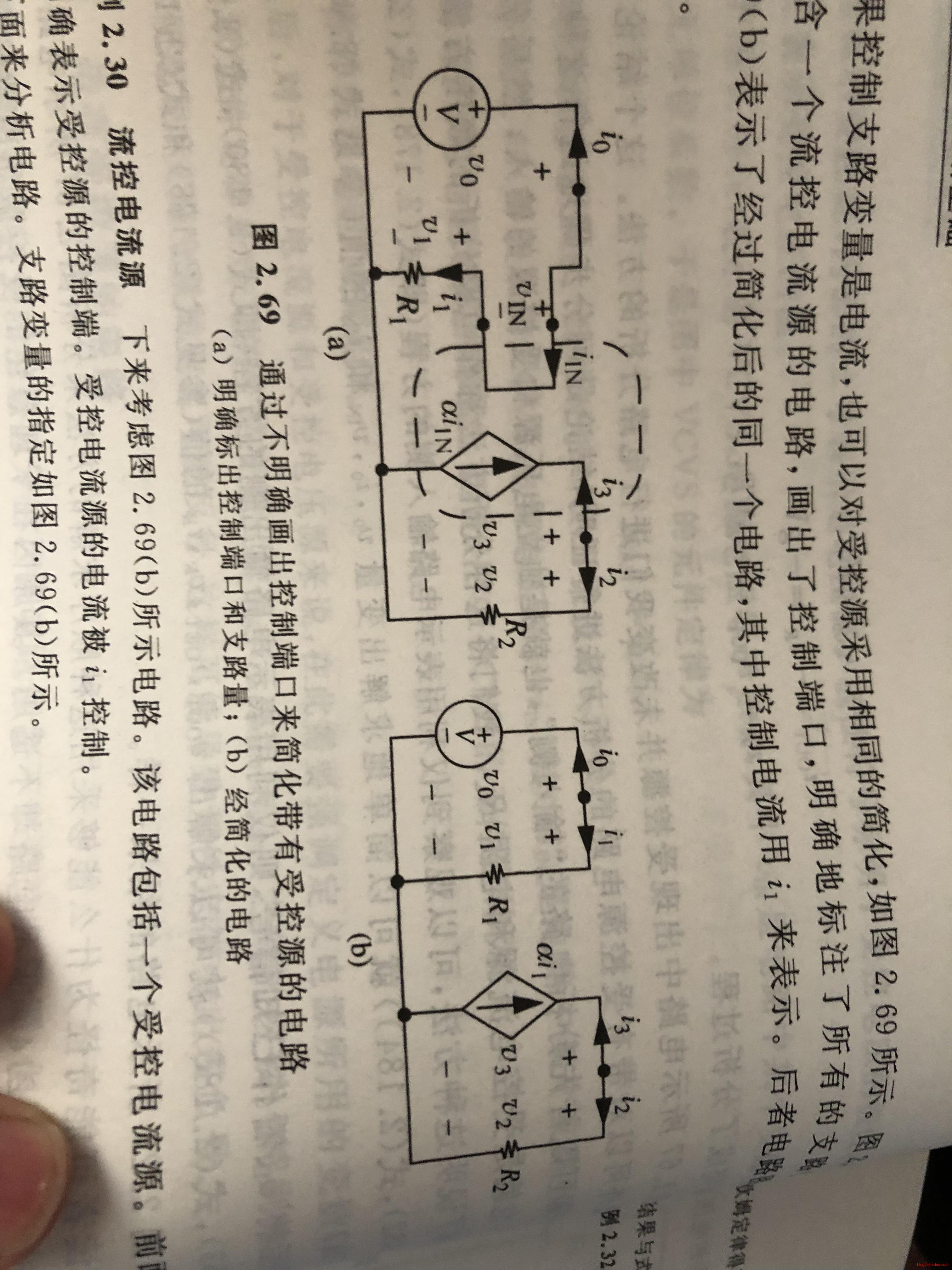
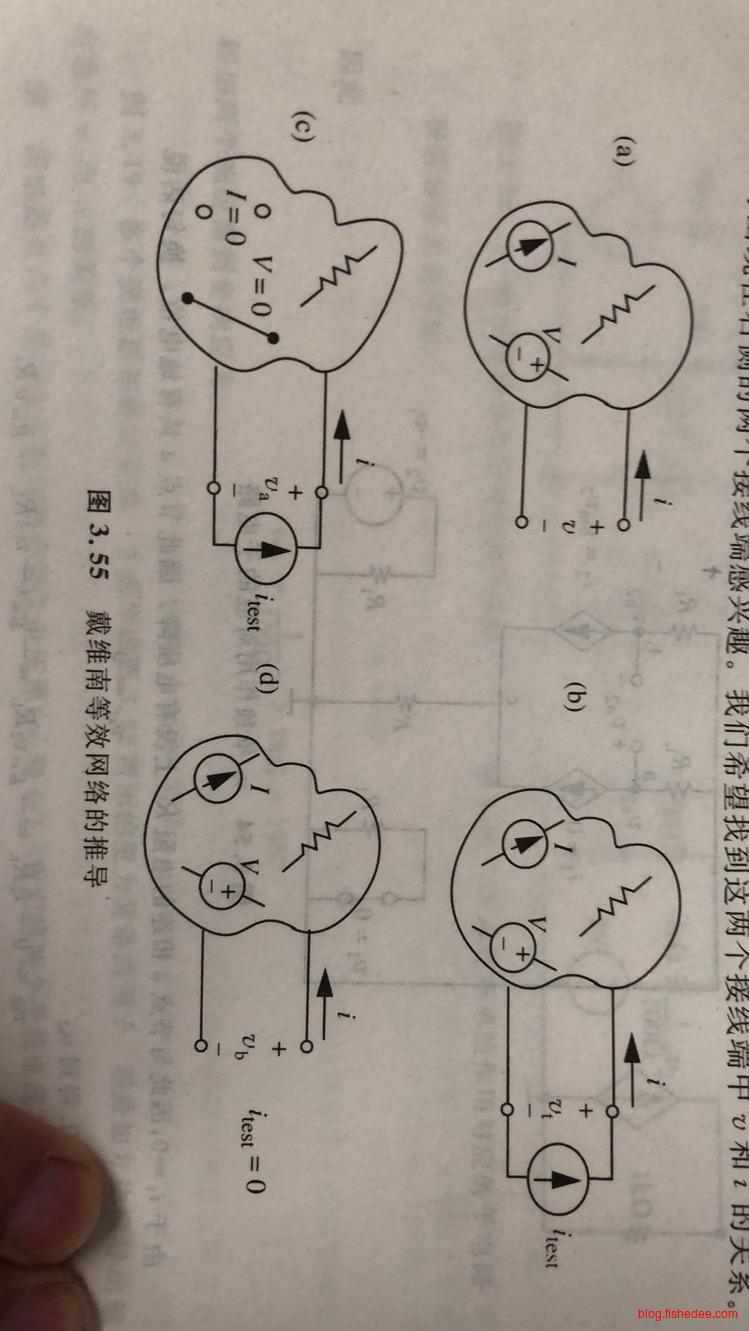
戴维南定理是通过叠加定理推导出来的,例如,假设我们要计算v端的电压值(a图),v端电压是假设在外部为电流源I驱动的(b图)。那么,根据叠加原理进一步推导,v端电压由两部分激励合起来的,要么是只有外部电流源I驱动的电路(c图)得到的电压值\(v_a\),要么是只有内部电源驱动的电路(d图)得到的电压值\(v_b\),也就是。
\[ v = v_a + v_b\\ v = v_{TH} + i_{test}R_{TH}\\ \]
既然我们推导出了,在任意的电流源下的电压响应。那么根据公式\(v = v_{TH} + i_{test}R_{TH}\),我们可以反向推导出等效的内部电路为:
4.3.2 一般例子
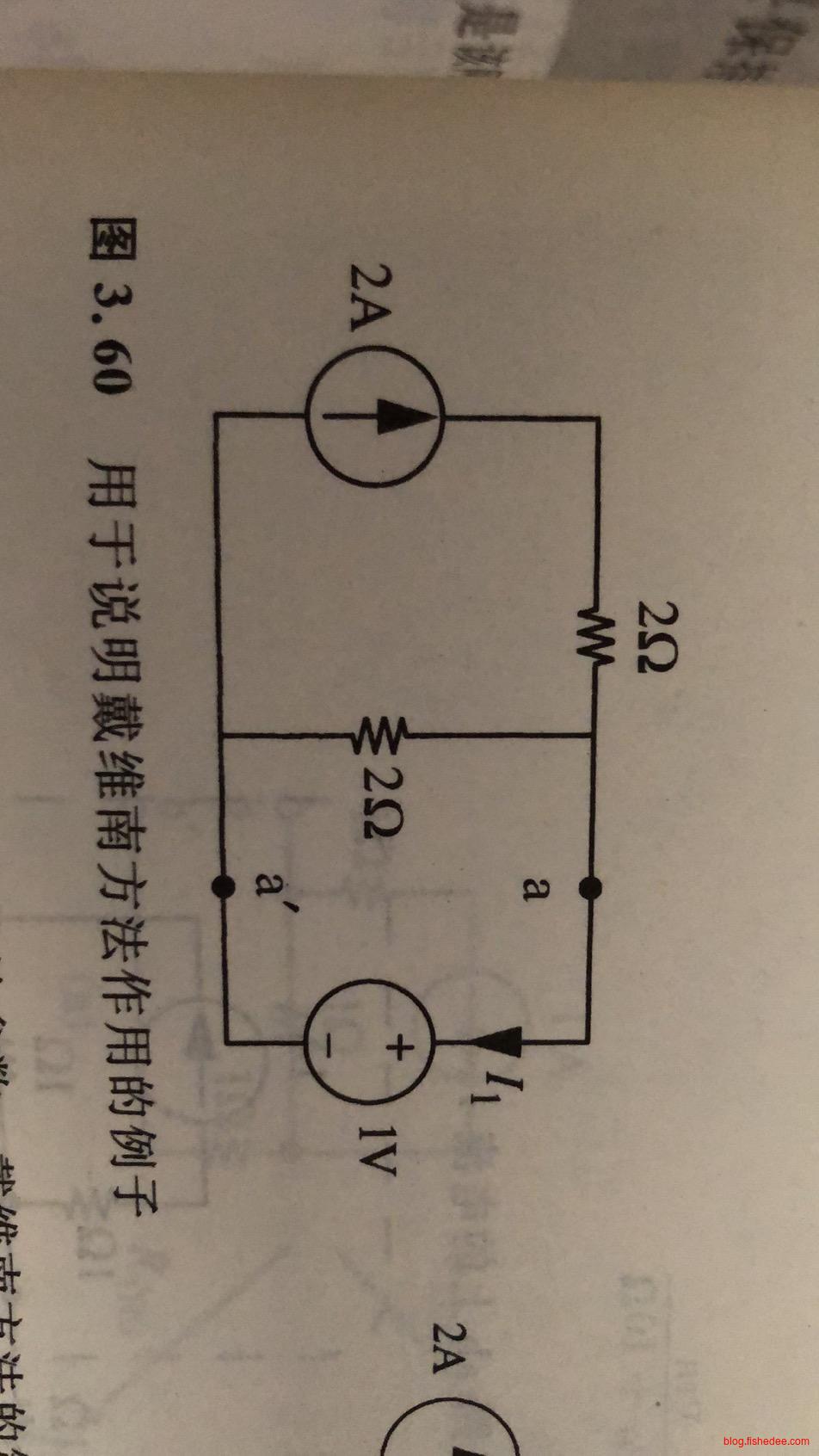
例如,我们要求的是电流\(I_1\)
我们可以先求戴维南等效电路的\(V_{TH}\)为\(2A\times 2 \Omega= 4V\)
然后求戴维南等效电路的\(R_{TH}\)为\(2\Omega\)
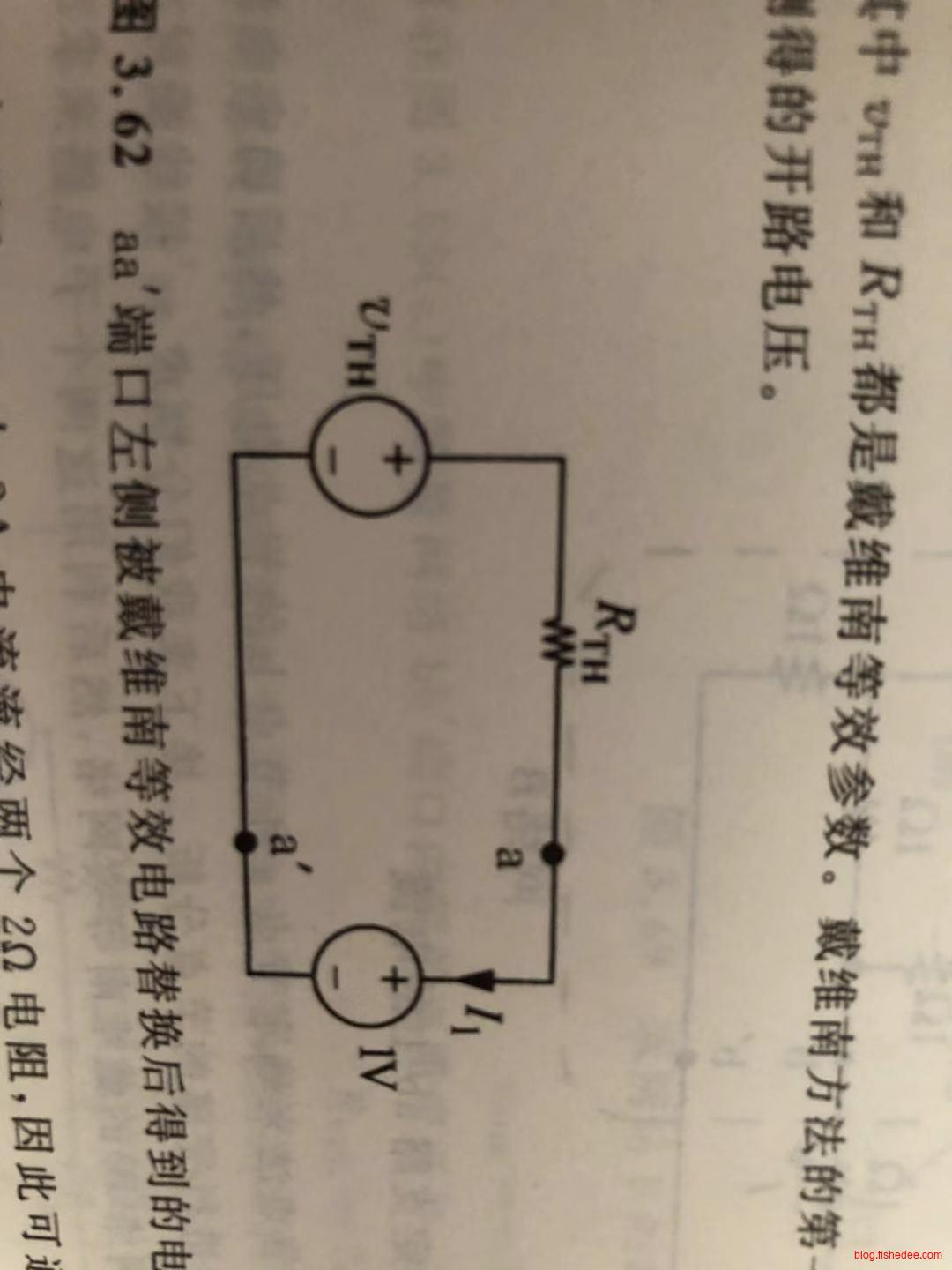
因此,有了等效电路后,我们可以轻松求解结果为:
\[ I_1 = \frac {4V -1V} {2\Omega} = \frac {3} {2}A \]
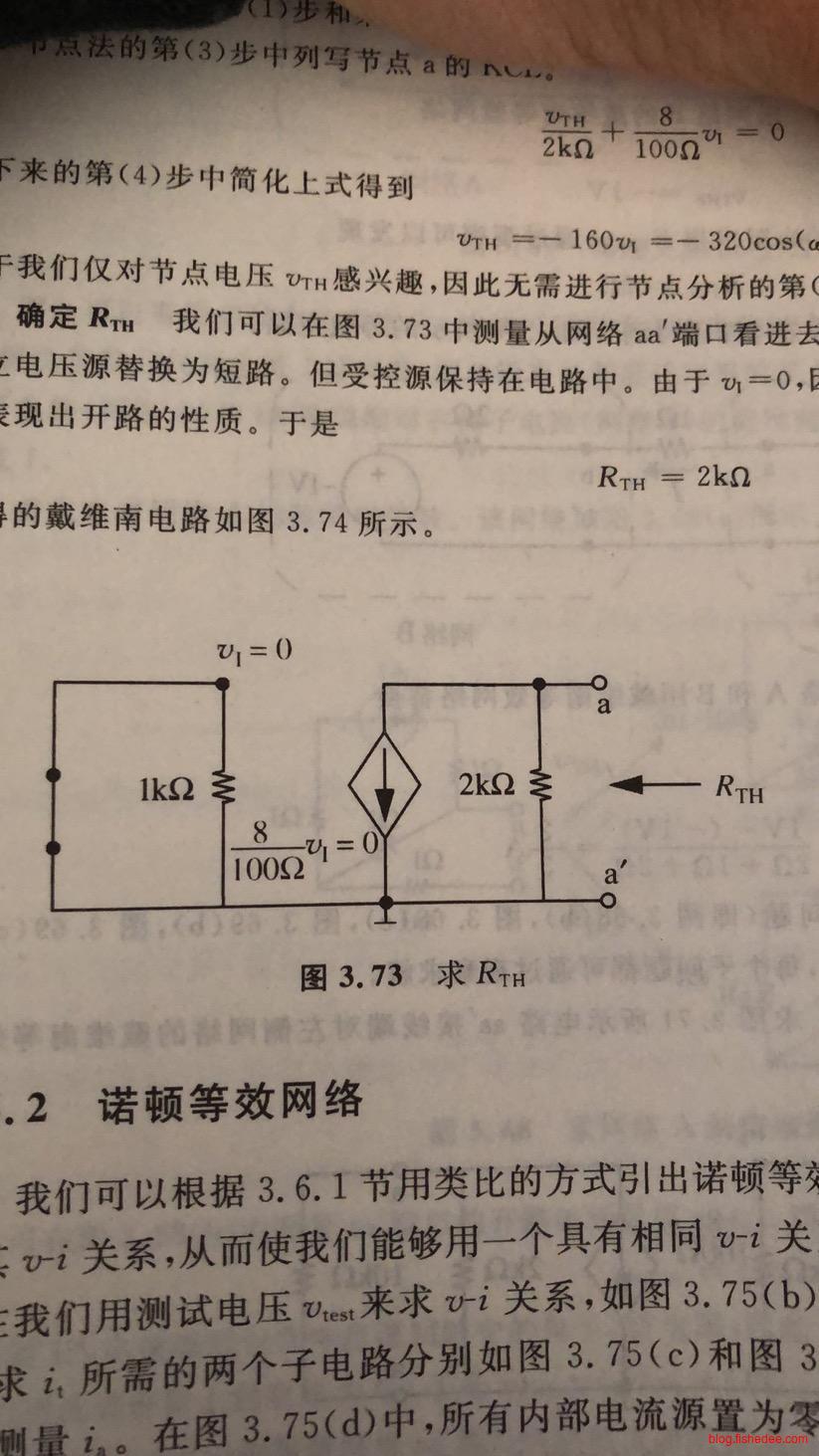
4.3.3 受控源的戴维南分析
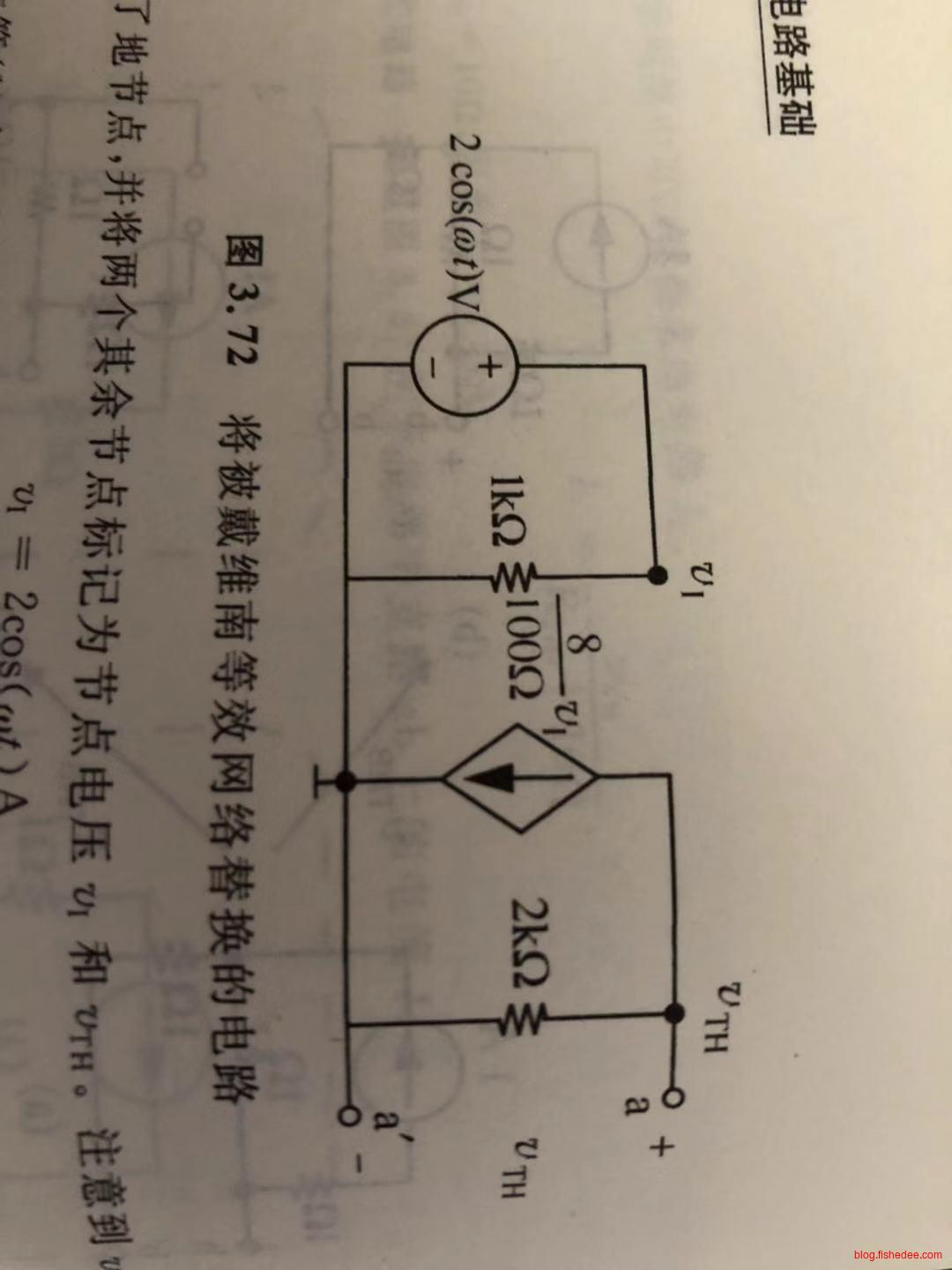
我们要将这个电路转换为戴维南电路,显然有
\[ \frac {v_{TH} - 0V} {2k\Omega} + I = 0\\ \frac {v_{TH} - 0V} {2k\Omega} + \frac {8} {100\Omega}v_i = 0\\ \frac {v_{TH} - 0V} {2k\Omega} + \frac {8} {100\Omega} 2cos(\omega t) = 0\\ v_{TH} = -320 cos(\omega t) V \]
另外,开路电阻显然为\(2k\Omega\)
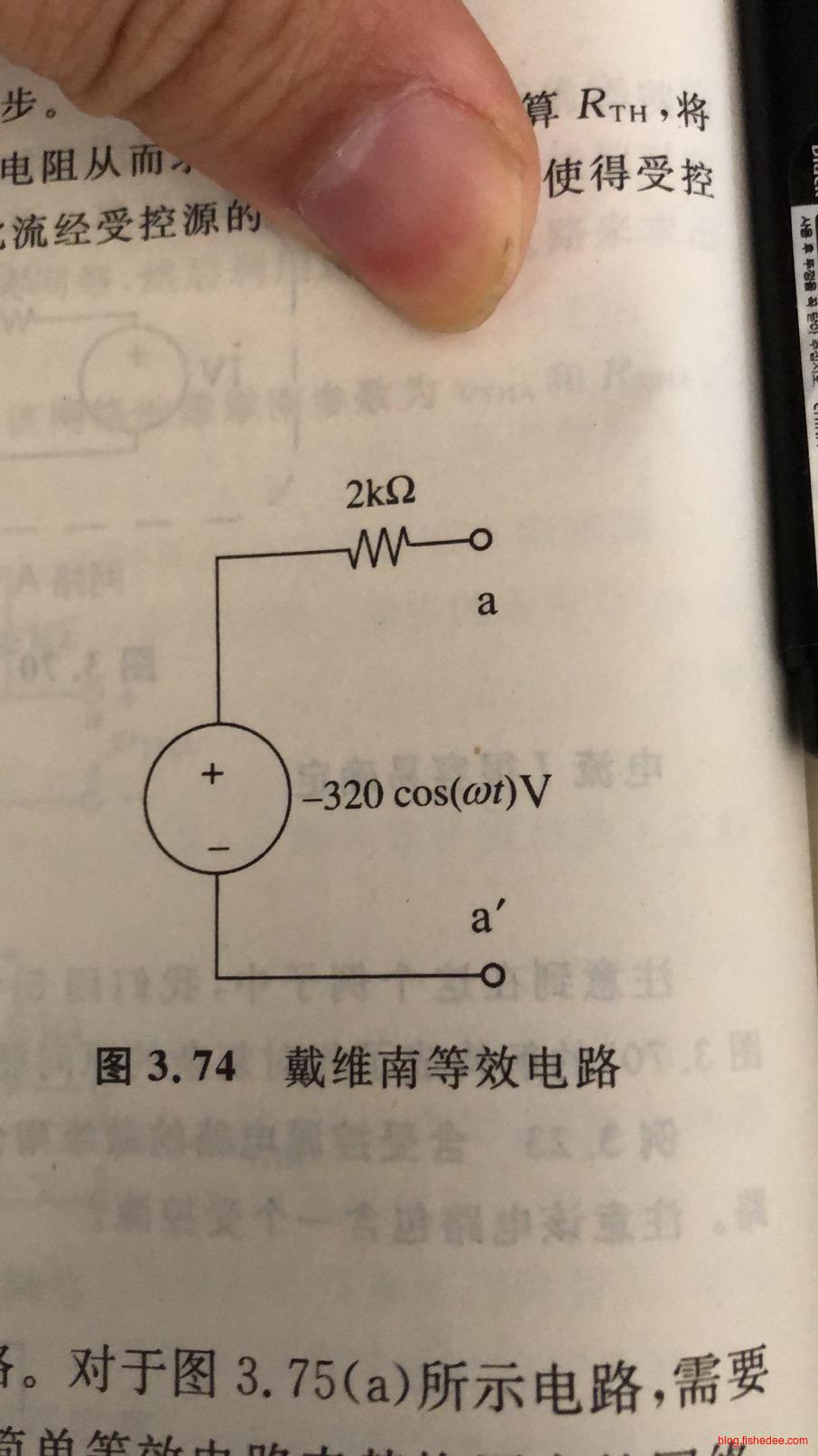
所以,整个受控电路的结果如上图
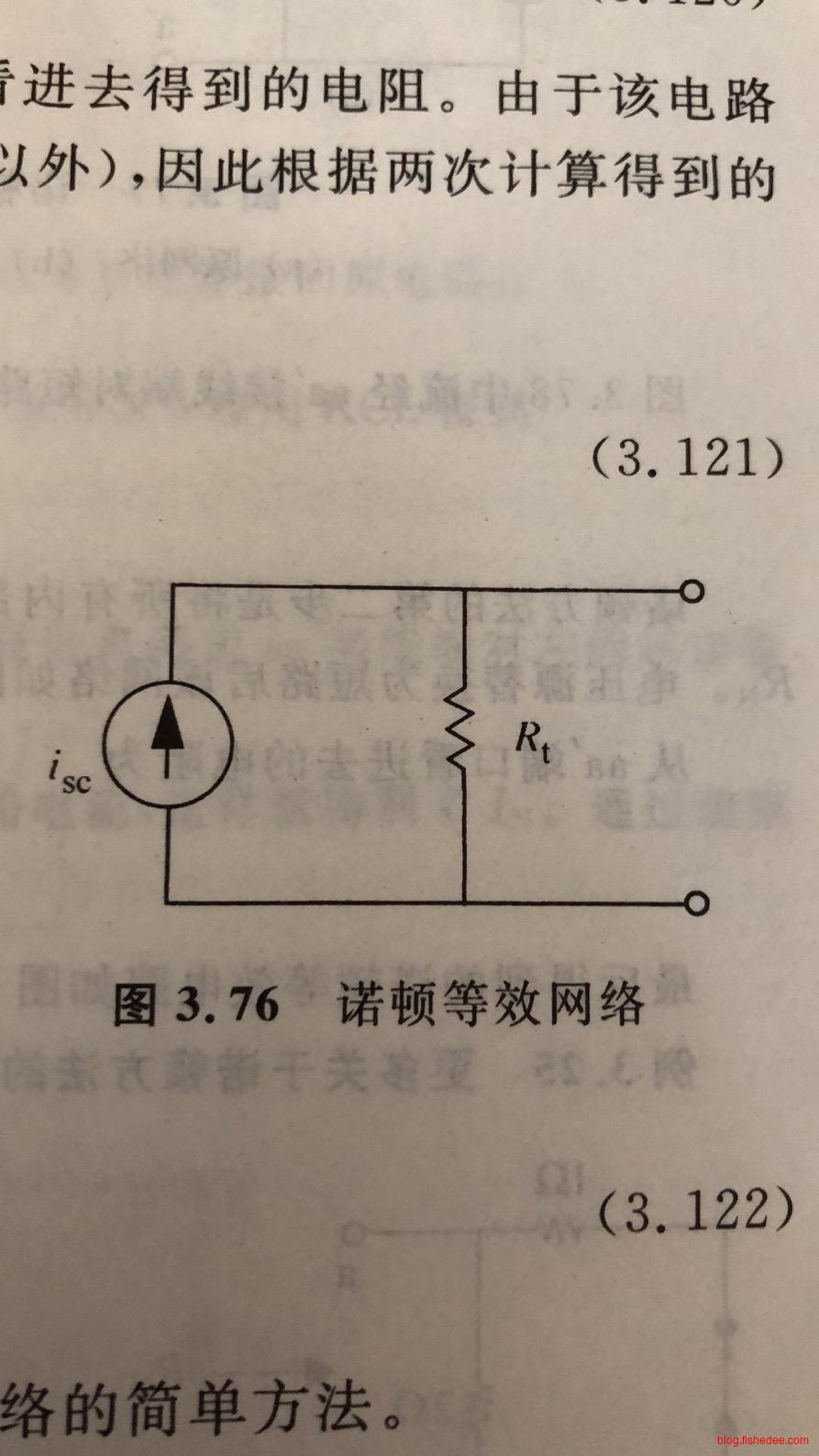
4.4.4 诺顿定理
诺顿定理为,任意线性网络在一对给定接线端上的诺顿等效电路包括一个电流源\(i_N\)和一个电阻\(R_N\)的并联。电流\(i_N\)和电阻\(R_N\)可通过下列方法获得
- \(i_N\)可通过原网络在给定接线端对上计算或测量短路电流得到
- \(R_N\)可通过将原网络内部所有独立源置为零后计算或测量从接线端对看进去的电阻得到。即用短路代替独立电压源,用开路来代替独立电流源,但是受控源需要保持不变。
可以看出,戴维南等效的\(R_{TH}\)与诺顿定理的\(R_N\)的获取方法是一样的,并且有以下关系:
\[ R_{TH} = \frac {v_{TH}} {i_N} \]
这意味着我们在获得一个等效电路以后,轻松计算到另外一个的等效电路。
5 非线性电路分析
非线性元件,就是接线端电流和接线端电压具有非线性代数关系的元件。
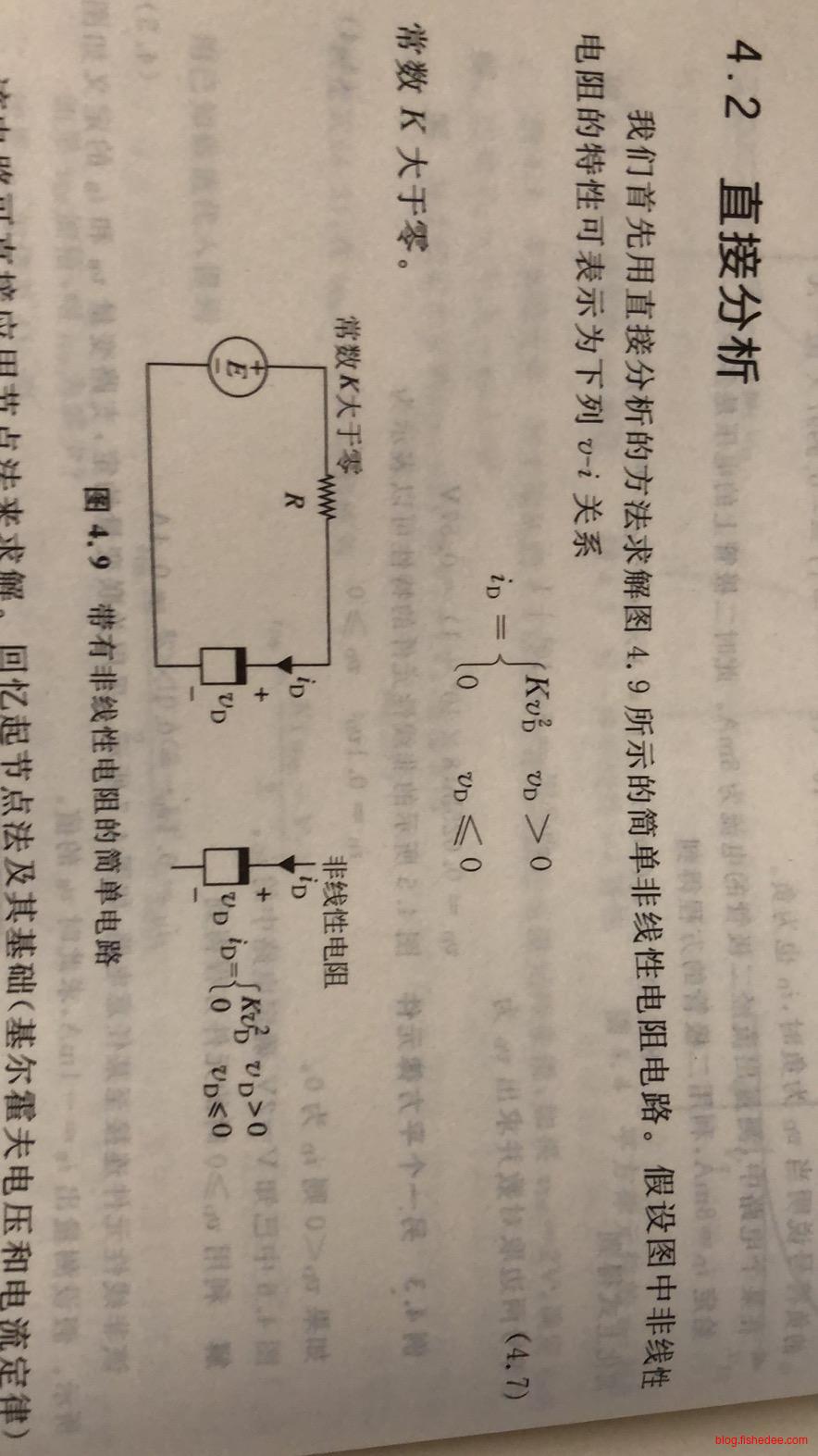
5.1 直接分析
直接分析,就是直接通过数学关系来求解电路和电流的关系。这种方法计算复杂,很少用到。
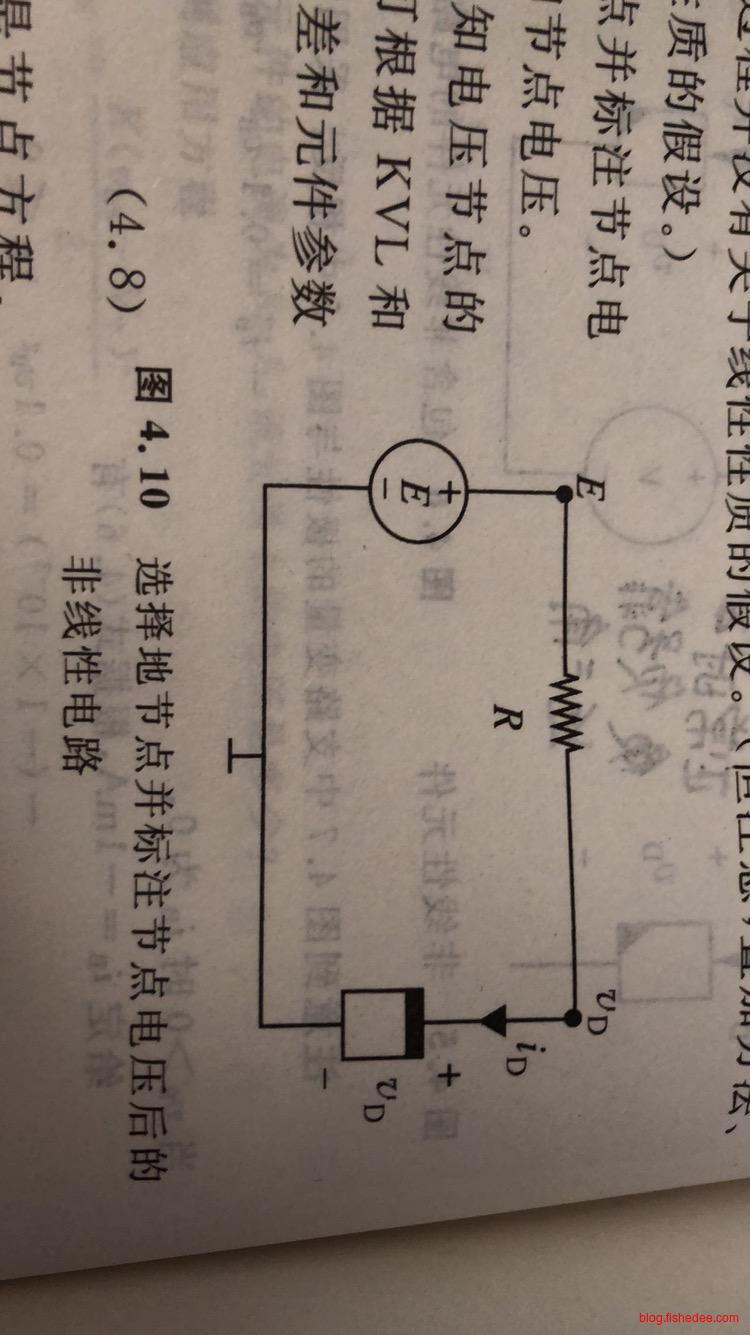
例如,我们可以用节点法,和数学关系来求解节点D的电压
\[ \frac {v_D - E} {R} + i_D = 0\\ \frac {v_D - E} {R} + Kv_D^2 = 0\\ RKv_D^2 + v_D -E =0\\ 显然,这是一个二次方程,取v_D为正数的解\\ v_D = \frac {-1 + \sqrt{1+4RKE}} {2RK} \]
5.2 图形分析
在绝大多数的情况下,我们都无法求解方程的解,当我们希望仅仅进行定量分析时,我们可以求助于图形分析。
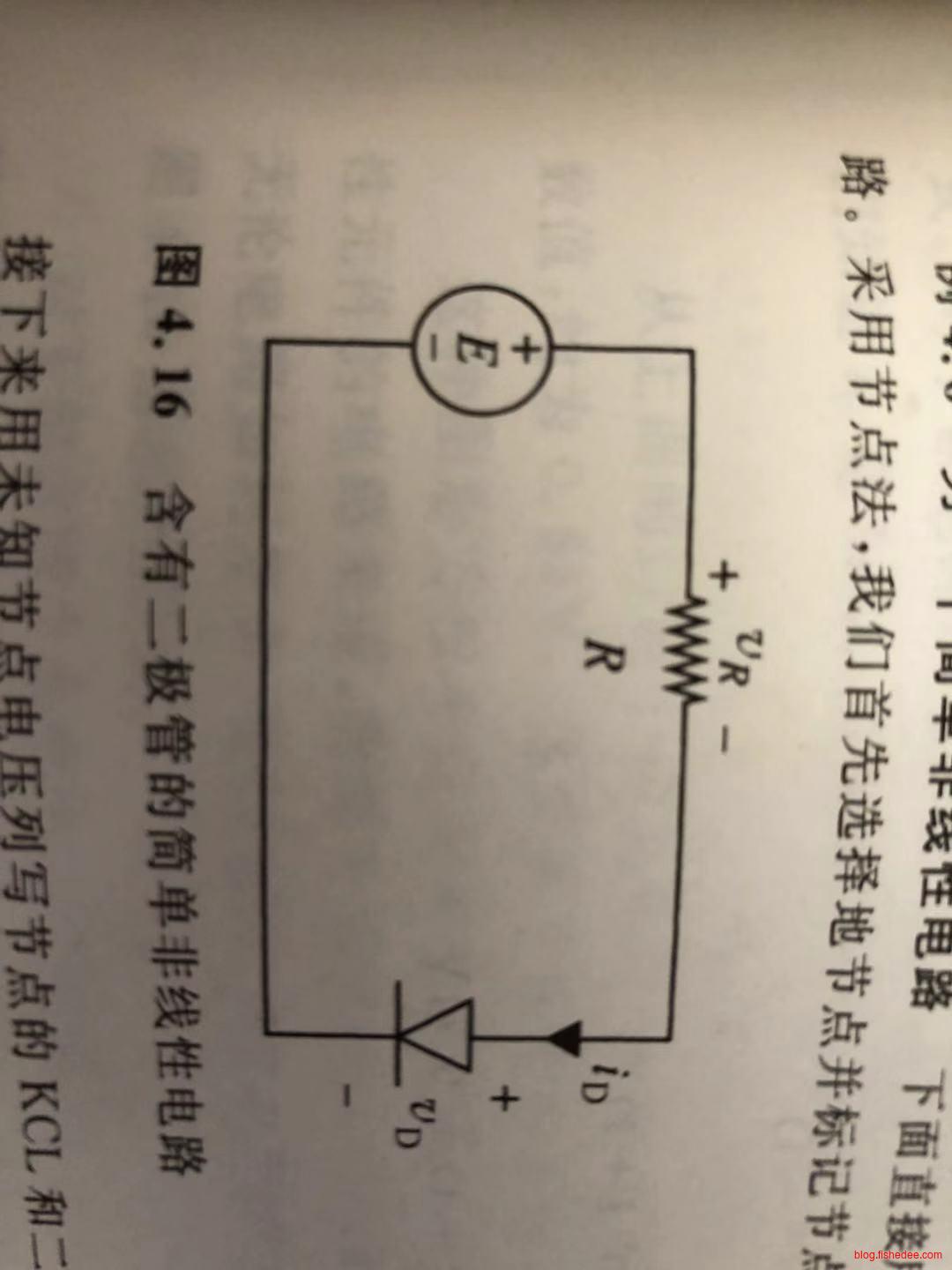
例如,对于不同的电压源E时,我们希望求得二极管两端的电压值。其中,二极管的方程为:
\[ i_D = I_s(e^{v_D/V_{TH}}-1) \]
另外,对于电阻,我们有
\[ R = \frac {E-v_D} {i_D}\\ i_D = -\frac {v_D-E}{R} \]
显然,对于电阻和二极管,我们列出了两个关于\(i_D\)和\(v_D\)的方程,直接法是直接求得两个方程的解,而图形法是画出这个曲线,取他们的交点,就是为解。
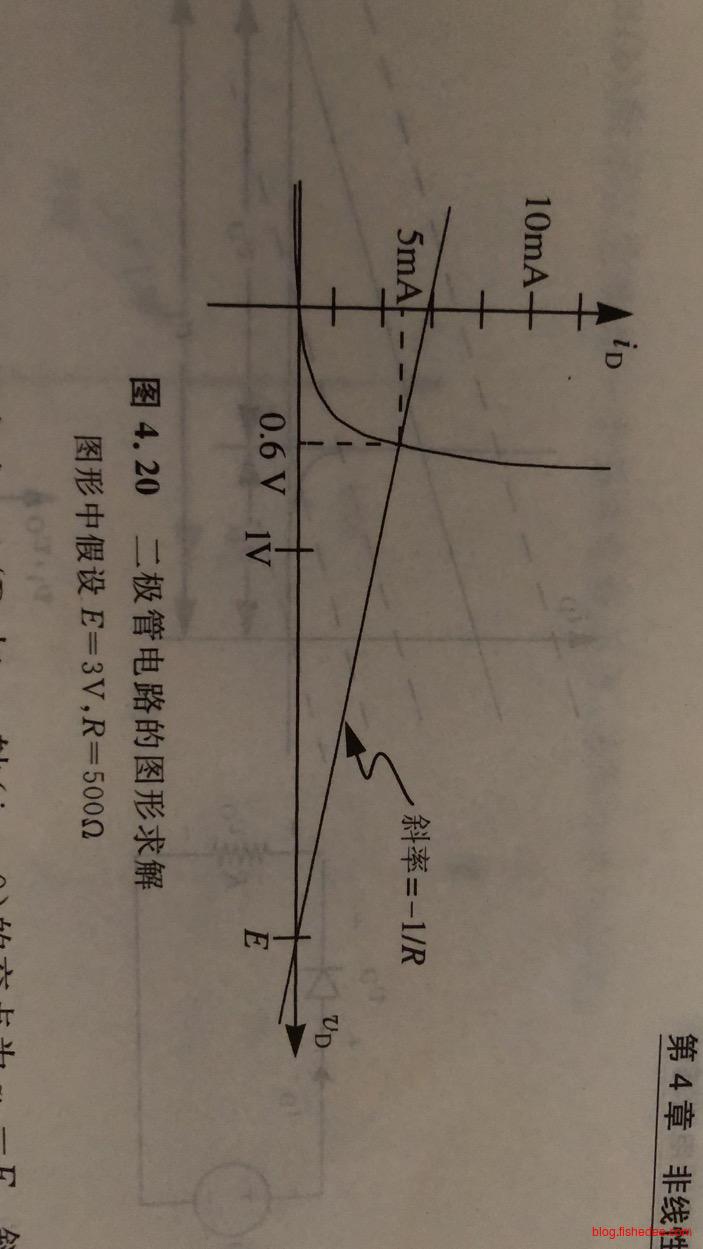
当我们画出不同的电压源E的曲线时,我们取到了不同的交点,我们就能得到以下结果:
- 当E比较大以后,二极管两端电压趋向于某个固定值,电阻两端电压接近于电源值E。
- 当E比较少以内,二极管两端电压占用了绝大部分的电压值,电阻两端电压的接近于0。
- 当E反向时,二极管两端电压就是为电源电压,电阻两端电压几乎为0。
5.3 分段线性分析
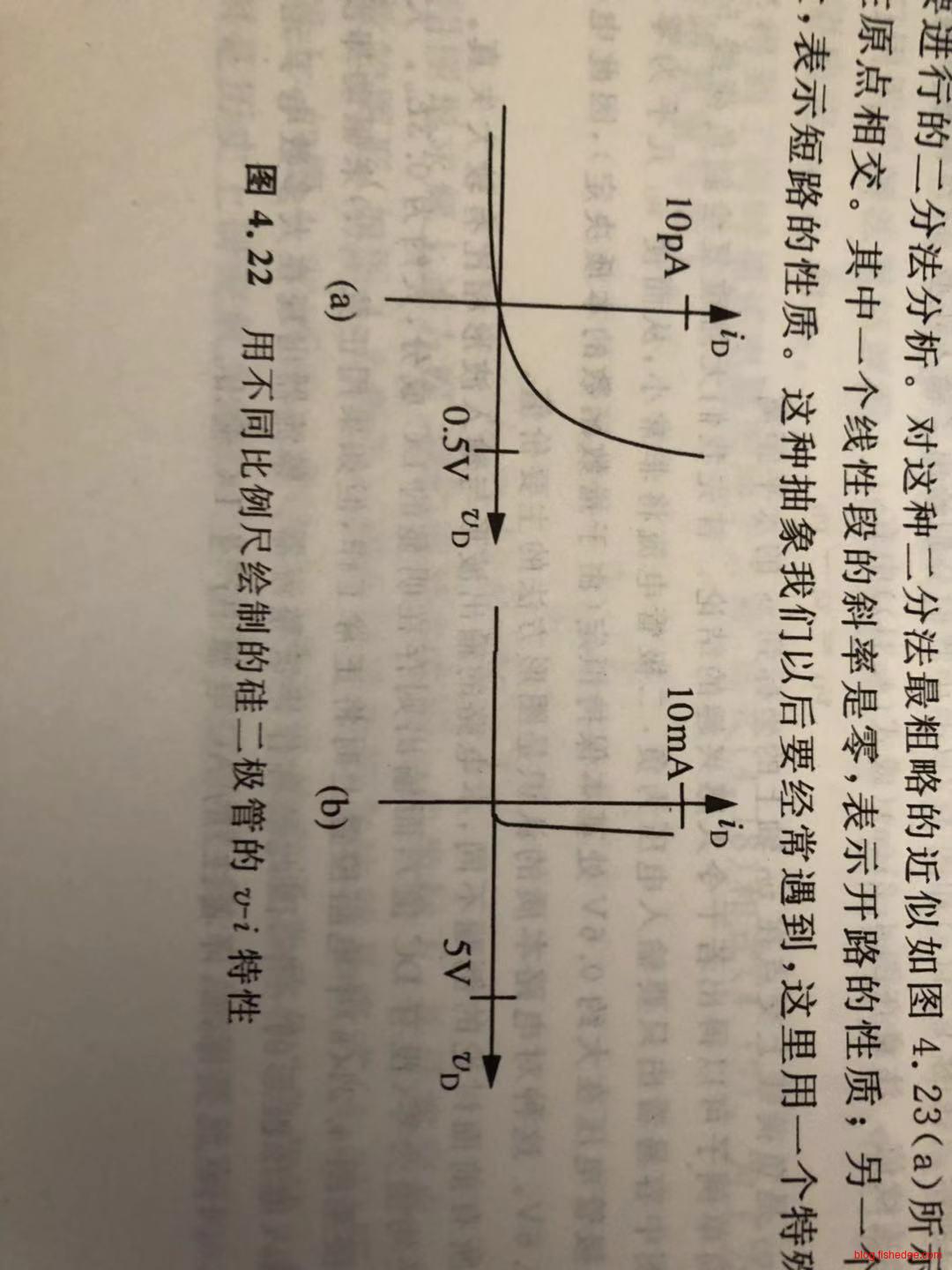
分段线性分析,就是在非线性元件上,用一系列直线段来表示其\(v-i\)特性。
例如,这是二极管的曲线图,二极管两端电压超过0.6V以后,就能产生较大的电流。
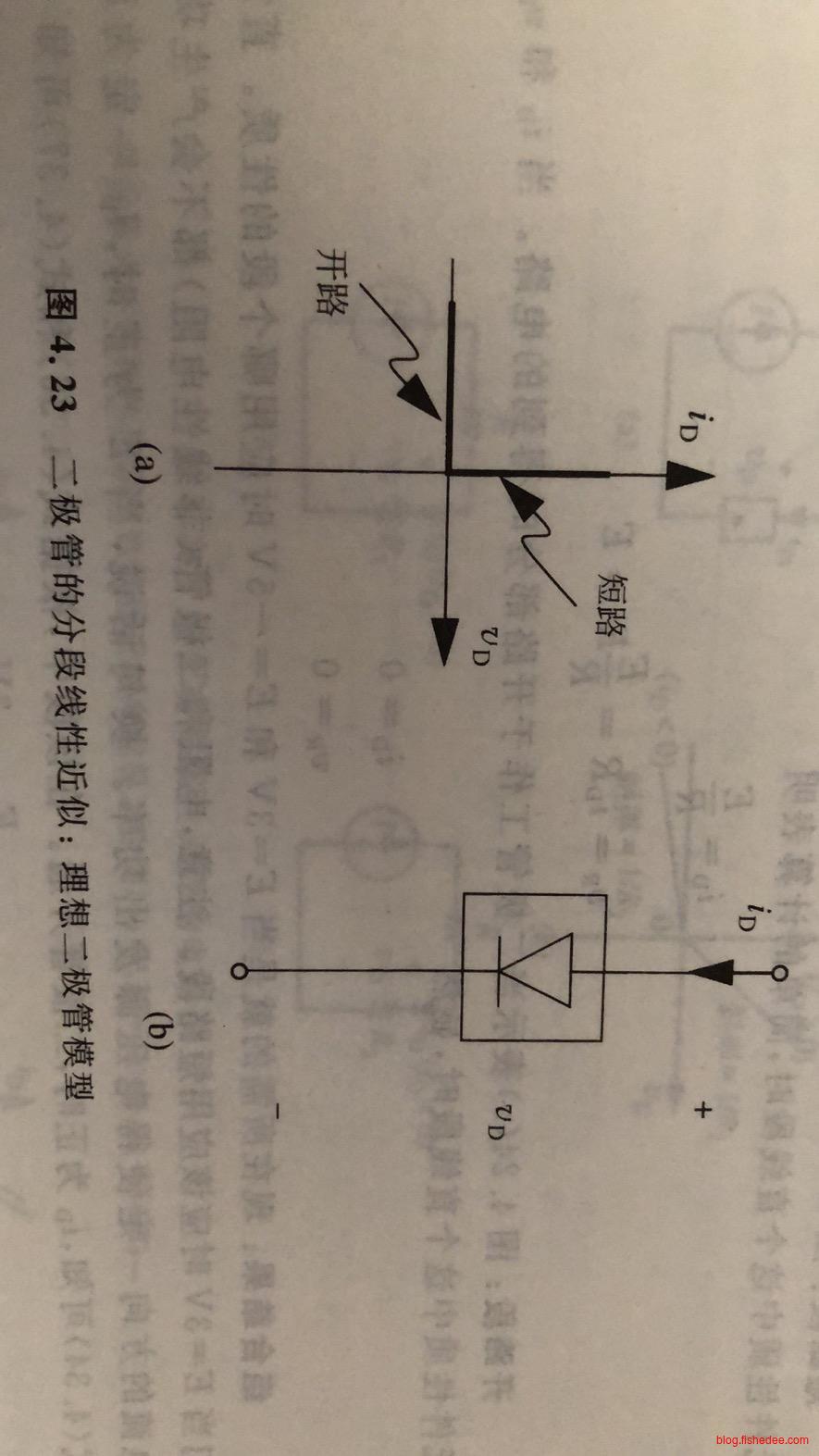
因此,我们可以用两条线段来近似这个曲线,正向电压时竖直的线段(开路),反向电压时横直的线段(断路),这个模型也被称为二极管的理想模型。
\[ 二极管=\begin{cases} v_D = 0,v_D为正时\\ i_D = 0,v_D为负时\\ \end{cases} \\ \]
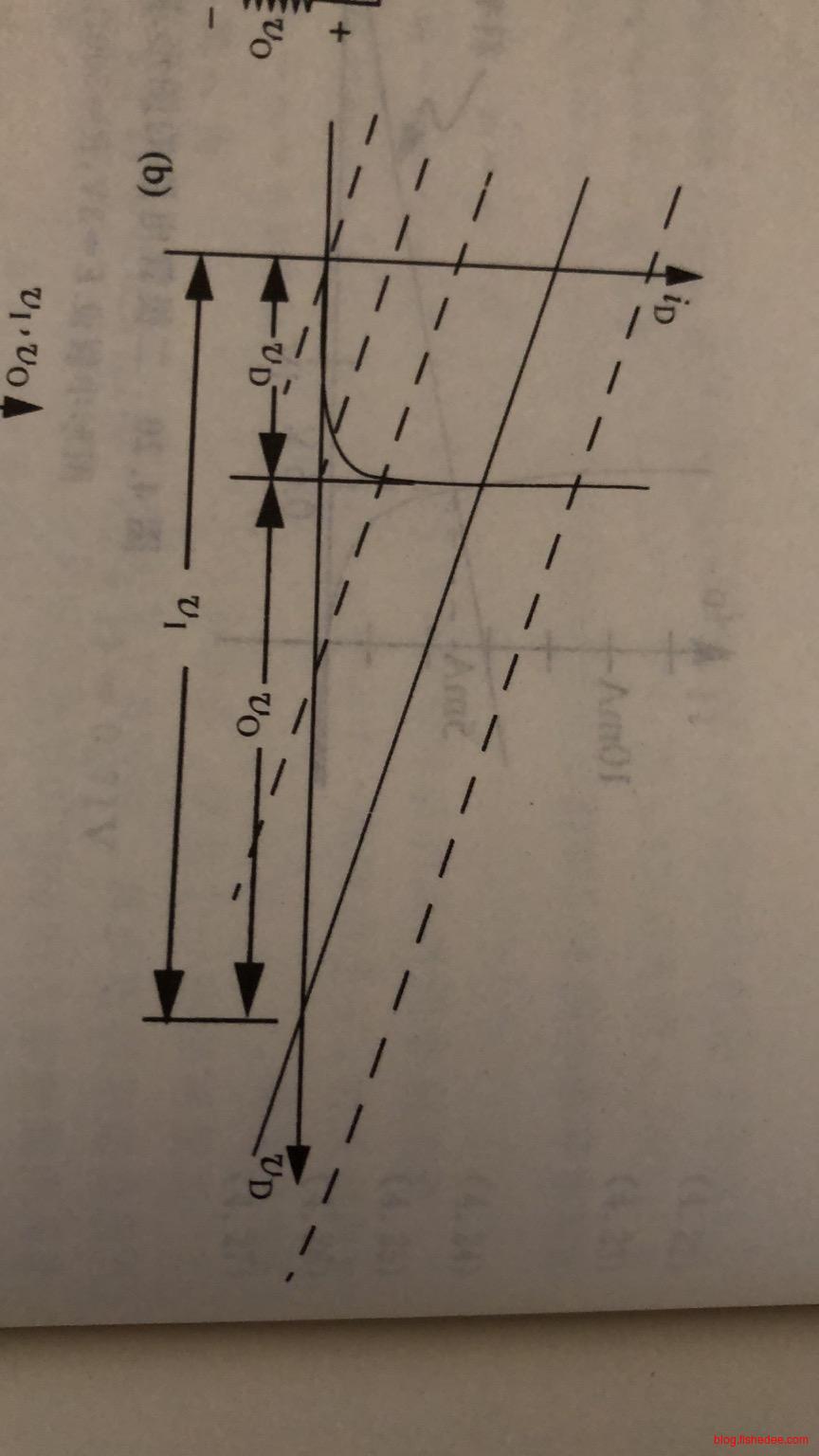
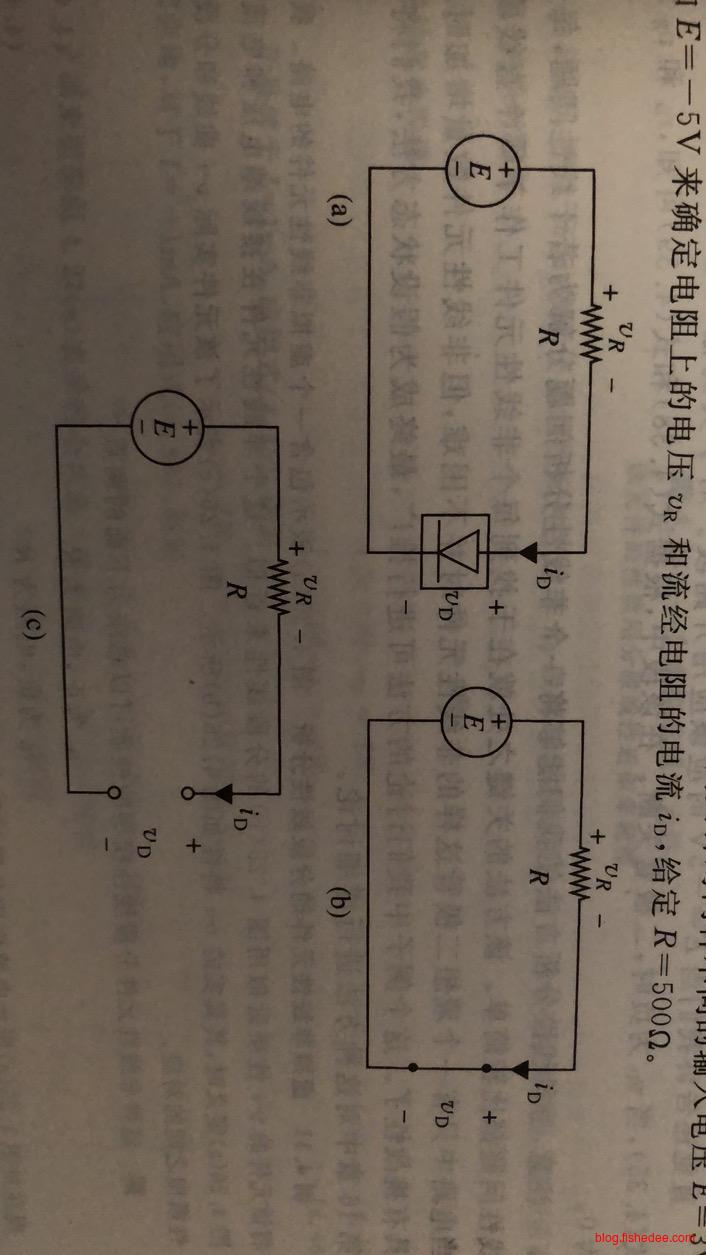
例如,对于a图,我们可以立即通过分段线性分析来得出在不同的E值时,对应的b图和c图
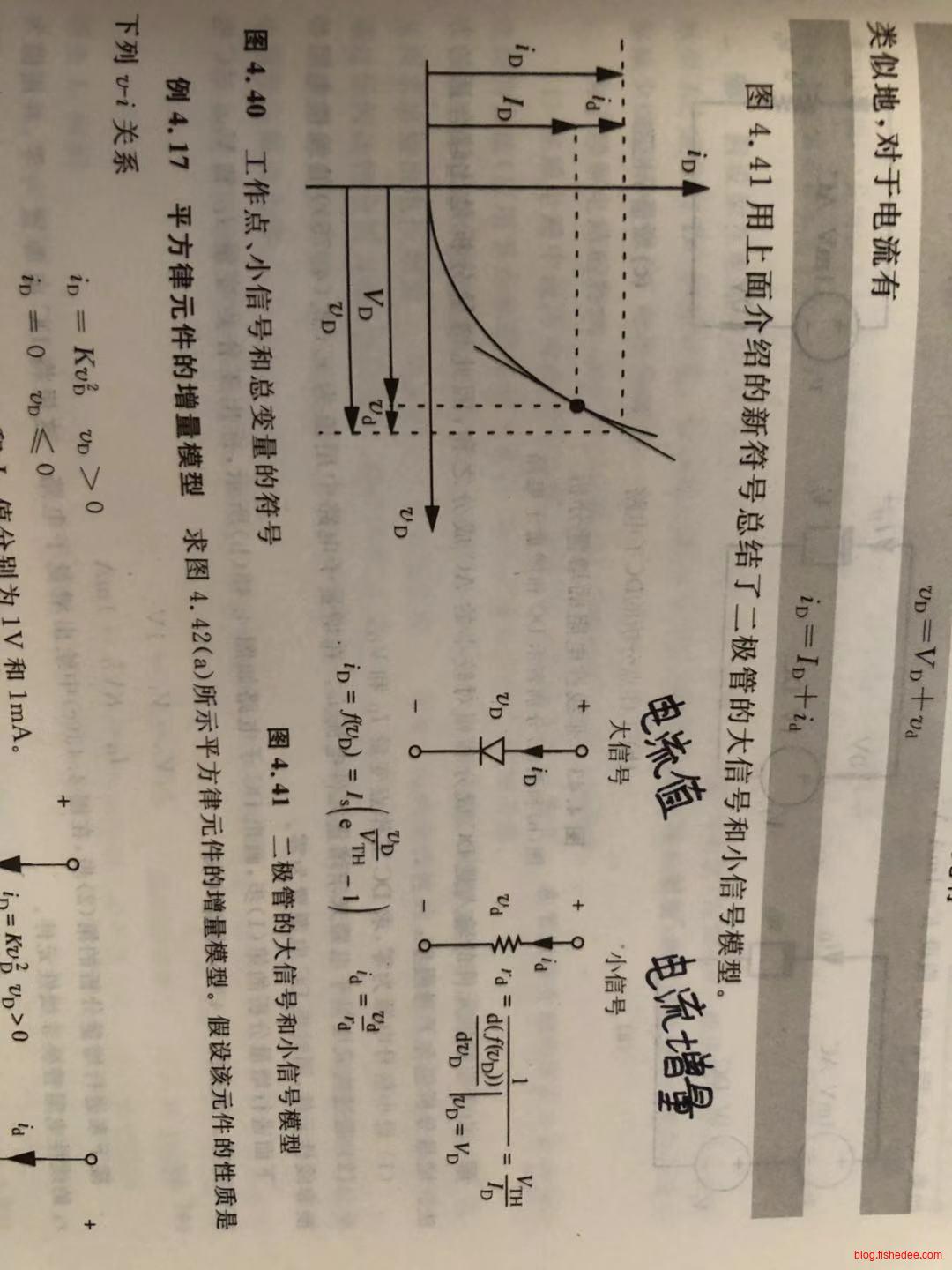
5.4 增量分析
5.4.1 一般步骤
当非线性元件仅在很小的电压和电流范围内运行时,图形分析无法进行定量分析,分段线性分析的分析太粗略,这个时候,我们可以求助于增量分析,也被称为大信号+小信号混合分析。注意,适用场景是,很小的电压和电流范围,而不是很小的电压和电流绝对幅值。
一般步骤为:
\[ r_d = \frac {1} {\frac {df} {dv_D}|_{v_D = V_D}} \]
- 在原电路中设所有小信号为零,根据得到的子电路求出DC工作点\(I_D\)和\(V_D\)。
- 将电路中的非线性元件替换为电阻\(r_d\),并将所有DC置为零(短路替换电压源,开路替换电流源)得到增量子电路,从而求得输出电压增量和电流增量。增量子电路是线性的,因此可以用任何线性分析方法来处理。
- 总电压和总电流就是由两个电路的结果相加得到的。
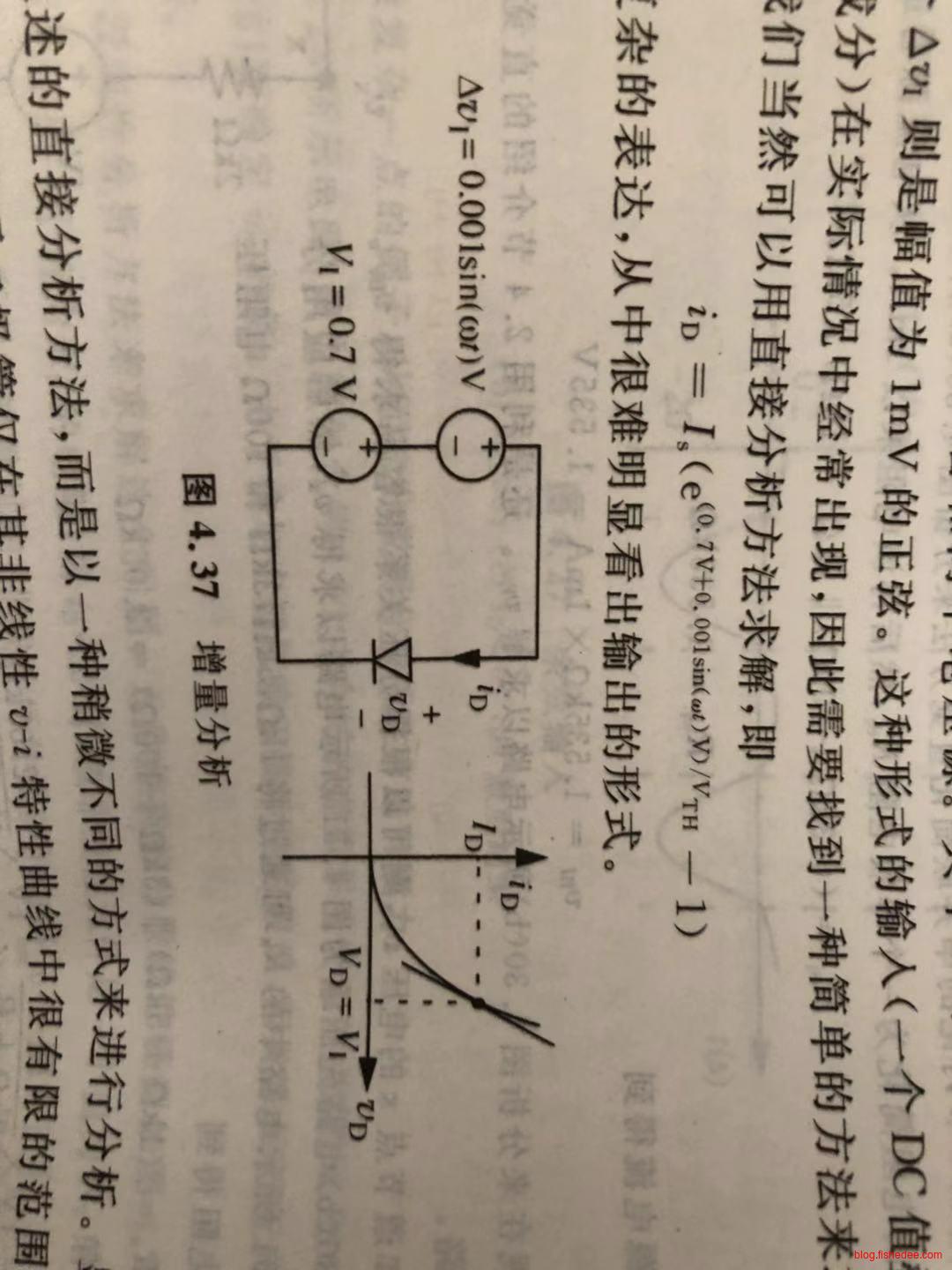
5.4.2 一般例子
例如,我们要计算二极管在0.7V+1mV正弦刺激下的电流是什么?
\[ 因为二极管方程为:i_D = I_s(e^{v_D/V_{TH}}-1)\\ 因此r_d = \frac {1} {\frac {df} {dv_D}|_{v_D = V_D}}\\ = \frac {1} {I_s\frac {1} {V_{TH}}(e^{v_D/V_{TH}})}\\ = \frac {1} {I_s\frac {1} {V_{TH}}(e^{v_D/V_{TH}})}\\ \approx \frac {1} {I_s\frac {1} {V_{TH}}(e^{v_D/V_{TH}}-1)}\\ = \frac {1} {\frac {i_D} {V_{TH}}}\\ = \frac {V_{TH}} {i_D} \]
也就是说
\[ 大信号下:I_D = 1.45A\\ 小信号下:I_d = \frac {V_d} {r_d}\\ = \frac {V_d} {\frac{V_{TH}} {I_D}} = 0.059sin(\omega t)A \]
这就是二极管的大信号和小信号的混合分析了
- 本文作者: fishedee
- 版权声明: 本博客所有文章均采用 CC BY-NC-SA 3.0 CN 许可协议,转载必须注明出处!